直線の方程式について学んでいきます。
・直線の方程式
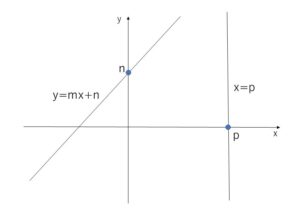
傾きが\(m\)で、\(y\)切片が\(n\)である直線の方程式は、\(y=mx+n\)・・・① です。
また①の形で表すことができない直線は、\(y\)軸に平行な直線(\(x\)軸に垂直な直線)であり、その方程式は\(x\)切片が\(p\)のとき、\(x=p\)・・・②となります。
なお傾き\(m\)が\(0\)のときは\(x\)軸に平行(\(y\)軸に垂直)な直線となり、①より\(y=n\) の形になります。また②で表される直線の傾きはありません。
直線は①②の形で表されるので、直線の方程式は\(x,y\)の1次式となります。
また、①は\(y\)の係数が\(0\)でなく、②は\(x\)の係数が\(0\)ではないので、定数\(a,b,c\)を用いて直線の方程式は一般に次のような形で表されます。
\(ax+by+c=0\) (\(a≠0\) または \(b≠0\))
では次に
(1)1点と傾きが分かっている場合 (2)2点が分かっている場合
の直線の方程式を求めてみます。
(1)
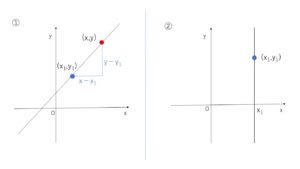
①傾きが\(m\)で\((x_1,y_1)\)を通る直線について
直線上の点を\((x,y)\)とすれば、傾き\(m\)は次のように表されます。
\(m=\displaystyle\frac{y-y_1}{x-x_1}\) (\(x≠x_1\))
よって直線の方程式は次のようになります。
\(y-y_1=m(x-x_1)\) (この式は\(x=x_1\)のときも成り立つ)
②\(x\)軸に垂直で\((x_1,y_1)\)を通る直線について
直線の\(x\)切片は\(x_1\)なので、直線の方程式は
\(x=x_1\) となります。
(2)
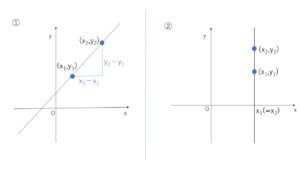
①2点\((x_1,y_1)\),\((x_2,y_2)\)を通る直線 (ただし\(x_1≠x_2\))
直線の傾き\(m\)は
\(m=\displaystyle\frac{y_2-y_1}{x_2-x_1}\)
また\((x_1,y_1)\)を通るので先ほどの(1)①より直線の方程式は
\(y-y_1=\)\(\displaystyle\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)
②2点\((x_1,y_1)\),\((x_2,y_2)\)を通る直線 (\(x_1=x_2\))
直線は\(x\)軸に垂直であり、\(x\)切片は\(x_1(=x_2)\)。 よって直線の方程式は
\(x=x_1\)
(例題)次の直線の方程式をそれぞれ求めよ。
(1)点\((-3,7)\)を通り、傾きが\(-2\)の直線
(2)2点\((4,-1)\),\((3,2)\)を通る直線
(3)2点\((-1,2)\),\((3,2)\)を通る直線
(4)2点\((4,1)\),\((4,5)\)を通る直線
(5)\(a≠0,b≠0\)のとき、\((a,0)\),\((0,b)\)を通る直線
2点が与えられたときは、\(x\)座標が同じかどうかに気を付けるとよいですが、機械的に傾きを求める①の公式を適用しても、\(x\)座標が同じ場合には分母が\(0\)になってしまうのでおかしいことにすぐに気づきます。
また余裕があれば1点を代入して方程式が成り立つかどうか検算するとよいでしょう。
(解答)
(1)
求める直線の方程式は
\(y-7=-2\{x-(-3)\}\)
よって \(y=-2x+1\)
(2)
求める直線の方程式は
\(y-(-1)=\displaystyle\frac{2-(-1)}{3-4}(x-4)\)
よって
\(y+1=-3(x-4)\) であるから
\(y=-3x+11\)
(3)
求める直線の方程式は
\(y-2=\displaystyle\frac{2-2}{3-(-1)}\{x-(-1)\}\)
よって \(y-2=0\) より
\(y=2\)
\(y=2\) としてもよいです。
(4)
2点の\(x\)座標が\(4\)で等しいので\(x\)軸に垂直な直線であり、求める方程式は
\(x=4\)
(5)
直線の方程式は
\(y-0=\displaystyle\frac{b-0}{0-a}(x-a)\)
よって \(\displaystyle\frac{y}{b}=-\displaystyle\frac{1}{a}(x-a)\) より
\(\displaystyle\frac{x}{a}+\displaystyle\frac{y}{b}=1\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→2直線の平行・垂直・一致 back→座標を用いた証明(点の座標)