定数\(k\)を含む直線の方程式に関する問題について見ていきます。
(例題)
直線 \(L:(k+2)x-y+2k-1=0\) (\(k\)は定数)と 点\(P(-3,0)\),\(Q(5,2)\) について
(1)\(k\)の値に関係なく\(L\)が通る定点の座標を求めよ。
(2)線分\(PQ\)(両端を含む)と\(L\)が共有点をもつような\(k\)の値の範囲を求めよ。
(3)どのように\(k\)を定めても\(L\)が通らない線分\(PQ\)上の点の座標を求めよ。
(解答)
(1)
直線\(L\)の方程式を\(k\)について整理すると
\(k(x+2)+2x-y-1=0\)
これが任意の\(k\)について成り立つ条件は
\(x+2=0\) かつ \(2x-y-1=0\)
この連立方程式を解くと \(x=-2\), \(y=-5\)
よって\(L\)が\(k\)の値によらず通る点は \((-2,-5)\)
(2)
すると線分\(PQ\)と共有点をもつときの境目が直線\(L\)が\(P\)または\(Q\)を通る時であることが分かります。
\(P,Q\)と(1)で求めた定点(\(R\)とする)を図示すると次の通り。
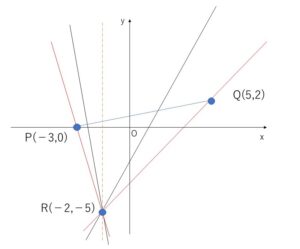
よって\(L\)が線分\(PQ\)と共有点をもつには
\(L\)の傾きが \(RP\)の傾き以下 または \(RQ\)の傾き以上
\(L:(k+2)x-y+2k-1=0\)の傾きは \(y=(k+2)x+2k-1\) より \(k+2\)で
\(RP\)の傾き\(=\displaystyle\frac{-5-0}{-2+3}\)\(=-5\)
\(RQ\)の傾き\(=\displaystyle\frac{2+5}{5+2}\)\(=1\)
ゆえに \(k+2≦-5\) または \(k+2≧1\)
したがって \(k≦-7\),\(k≧-1\)
(3)
\(L:y=(k+2)x+2k-1\)より、\(R\)を通る\(x\)軸に垂直な直線 \(x=-2\)です。
\(k\)について整理した \(k(x+2)+2x-y-1=0\) からも、\(k\)でくくられた部分の \(x+2=0\) が表すことができない直線であることが分かります。
\(L:y=(k+2)x+2k-1\)より、\(k\)をどのように定めても、\(L\)は\(R\)を通る\(x\)軸に垂直な直線 \(x=-2\) を表すことができない。
よって求める点の座標は、線分\(PQ\)と\(x=-2\)の交点である。
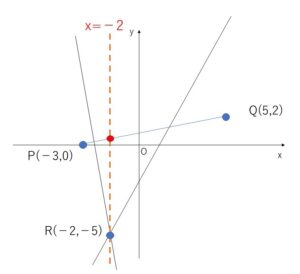
直線\(PQ\)の方程式は
\(y=\displaystyle\frac{1}{4}(x+3)\) であり
\(x=-2\)を代入して \(y=\displaystyle\frac{1}{4}\)
よって \((-2,\displaystyle\frac{1}{4})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→点と直線の距離 back→2直線の交点を通る直線