点と直線の距離を求める公式にについて見ていきます。
・点と直線の距離
点\(P\)と直線\(l\)の距離は、\(P\)から\(l\)に下した垂線を\(PH\)とすると、線分\(PH\)の長さになります。
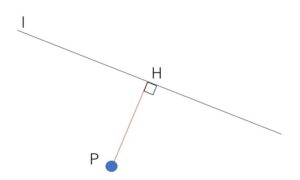
では座標平面上において、直線 \(l:ax+by+c=0\) (\(a≠0\) または \(b≠0\))と \(P(x_1,y_1)\)の距離\(d\)を考えていきます。
②\(H\)の座標を求める
③\(PH\)の距離を求める
という流れになりますが、簡単にするために\(P\)が原点にくるように全体を平行移動させます。すると\(l\)に垂直な直線は原点を通る直線になり、距離\(d\)は、\(H\)の移動先を\(H'(x_0,y_0)\)とすると\(d=\sqrt{x_0^2+y_0^2}\) になり簡単になります。
\(l:ax+by+c=0\)と\(P(x_1,y_1)\)を、\(P\)が原点にくるように\(x\)軸方向に\(-x_1\),\(y\)軸方向に\(-y_1\)平行移動させると、
直線は \(l’:\) \(a(x+x_1)+b(y+y_1)+c=0\)・・・(ア) となり、
\(H\)が移った点を\(H’\)とすると、距離\(d\)は原点と\(H’\)の距離となります。
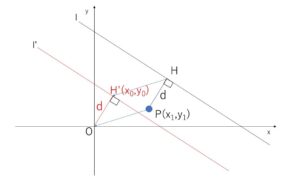
(ア)は \(ax+by+(ax_1+by_1+c)=0\) であり、原点を通り\(l’\)に垂直な直線は \(bx-ay=0\)・・・(イ) なので、(ア)(イ)を連立して解くと\(H’\)の座標が求まります。
簡単のため(ア)の定数部分を \(ax_1+by_1+c=k\) とおくと
\(ax+by+k=0\)・・・(ア) と \(bx-ay=0\)・・・(イ) の交点\(H’\)の座標は
(ア)×a+(イ)×bと (ア)×b-(イ)×a より
\(H'(-\displaystyle\frac{ka}{a^2+b^2},-\displaystyle\frac{kb}{a^2+b^2})\)
したがって
\(d=OH’\)
\(=\sqrt{(-\displaystyle\frac{ka}{a^2+b^2})^2+(-\displaystyle\frac{kb}{a^2+b^2})^2}\)
\(=\sqrt{\displaystyle\frac{k^2}{a^2+b^2}}\)
\(=\displaystyle\frac{|k|}{\sqrt{a^2+b^2}}\)
\(=\)\(\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(d=\)\(\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
分子の絶対値の中身は直線の式\(ax+by+c=0\)に\((x_1,y_1)\)を代入したものなので比較的覚えやすい思います。
(例題)
(1)点\((-3,-5)\)と直線 \(2x-4y+1=0\) の距離を求めよ。
(2)2つの直線 \(3x+4y=4\) と \(3x+4y=14\) との距離を求めよ、
(3)点\((5,-1)\)と 直線 \(ax-4y-4=0\) (\(a\)は正の定数) との距離が\(3\)のとき、\(a\)の値を求めよ。
(解答)
(1)
点\((-3,-5)\)と直線 \(2x-4y+1=0\) の距離\(d\)は
\(d=\displaystyle\frac{|2・(-3)-4・(-5)+1|}{\sqrt{2^2+(-4)^2}}\)\(=\displaystyle\frac{15}{\sqrt{20}}\)\(=\)\(\displaystyle\frac{3\sqrt{5}}{2}\)
(2)
2直線は平行なので、一方の直線のある1点をどこでもよいのでとって、その点ともう一方の直線との距離を求めます。
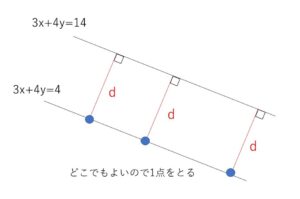
\(3x+4y=4\) は \((0,1)\)を通るので求める距離\(d\)は、\(3x+4y=14\) (\(3x+4y-14=0\))と \((0,1)\)の距離である。
\(d\)\(=\displaystyle\frac{|3・0+4・1-14|}{\sqrt{3^2+4^2}}\) \(=\displaystyle\frac{10}{5}=\)\(2\)
(3)
点\((5,-1)\)と 直線 \(ax-4y-4=0\) (\(a\)は正の定数) との距離が\(3\)なので
\(\displaystyle\frac{|5a+4-4|}{\sqrt{a^2+16}}\)\(=3\) (左辺の分母は\(0\)にならない)
よって \(|5a|=3\sqrt{a^2+16}\)
両辺正なので2乗して
\(25a^2=9(a^2+16)\)
\(a^2=9\) より \(a=±3\)
\(a>0\) なので \(a=3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の面積 back→定点を通る直線