三角形を分ける直線に関する問題について見ていきます。
(例題)
3点 \(A(0,1)\), \(B(0,\displaystyle\frac{3}{2})\), \(C(1,0)\) を頂点とする三角形を、原点を通る直線で切り、その面積を2等分する直線の傾きを求めよ。
(解答)
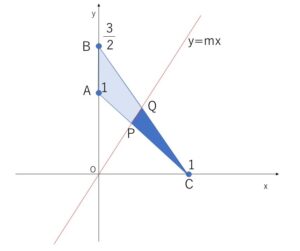
原点を通る直線を \(y=mx\)・・・①とおく。\(△ABC\)を2等分するので、\(m>0\)。
直線\(AC\)の方程式は \(y=-x+1\)・・・②
直線\(BC\)の方程式は \(y=-\displaystyle\frac{3}{2}x+\displaystyle\frac{3}{2}\)・・・③
\(AC\),\(BC\) と \(y=mx\)の交点を\(P,Q\)とすると、\(P,Q\)の座標は①②、①③を連立して求めると
\(P(\displaystyle\frac{1}{m+1},\displaystyle\frac{m}{m+1})\), \(Q(\displaystyle\frac{3}{2m+3},\displaystyle\frac{3m}{2m+3})\)
また\(△ABC=\displaystyle\frac{1}{2}・(\displaystyle\frac{3}{2}-1)・1\)\(=\displaystyle\frac{1}{4}\) より、2等分された図形の面積はそれぞれ \(\displaystyle\frac{1}{8}\)
よって、\(△CPQ=\displaystyle\frac{1}{8}\)
\(△CPQ=△OQC-△OPC\) を利用してみます。
\(△CPQ=△OQC-△OPC\) より
\(\displaystyle\frac{1}{8}\)\(=\displaystyle\frac{1}{2}・1・\displaystyle\frac{3m}{2m+3}\) \(-\displaystyle\frac{1}{2}・1・\displaystyle\frac{m}{m+1}\)
よって
\(\displaystyle\frac{1}{4}=\displaystyle\frac{m^2}{(m+1)(2m+3)}\)
整理すると
\(2m^2-5m-3=0\)
\((2m+1)(m-3)=0\)
\(m>0\) より \(m=3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→座標を利用した証明(直線の方程式) back→曲線と直線の距離