2直線の平行・垂直・一致

2直線の特徴的な関係(平行・垂直・一致)について見ていきます。

・2直線の平行・垂直 (\(y=mx+n\)型)
平面上の2直線は、1点で交わるか、平行であるか、一致するかのいずれかになりますが、このうち平行・一致と、1点で垂直に交わる場合について考えていきます。

まずは平行・一致について
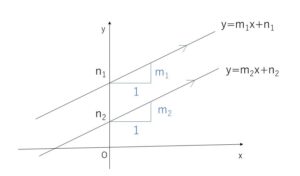
2直線
\(y=m_1x+n_1\)
\(y=m_2x+n_2\)
が平行であるとき、それぞれの直線の傾きが等しいときなので、
\(m_1=m_2\)
また、逆に\(m_1=m_2\)のときは2直線は平行になります。

なお、さらに\(n_1=n_2\)のときは2直線はぴったり重なる、つまり一致しますが、このときも平行であることにします。

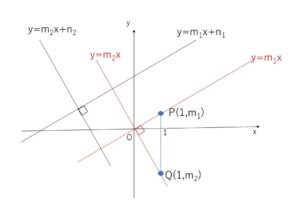
次に垂直に交わる場合について
2直線
\(y=m_1x+n_1\)
\(y=m_2x+n_2\)
について、2直線の交点が原点にくるように直線を平行移動させると、もとの2直線が垂直に交わるとき、平行移動後の2直線 \(y=m_1x\),　\(y=m_2x\) も垂直に交わることになります。
よって図のように\(P(1,m_1)\),\(Q(1,m_2\))をとると、三平方の定理から

\(OP^2+OQ^2=PQ^2\)
よって
\((1+m_1^2)+(1+m_2^2)\)\(=(m_2-m_1)^2\)・・・(A)
整理すると
\(m_1m_2=-1\)
また、逆に\(m_1m_2=-1\)のとき(A)が成り立つ、つまり\(OP^2+OQ^2=PQ^2\)が成り立つことになるので、2直線は垂直に交わります。

・2直線の平行・垂直 (\(ax+by+c=0\)型)
上の結果を用いて
2直線
\(a_1x+b_1y+c_1=0\)　(\(a_1≠0\) または \(b_1≠0\))・・・①
\(a_2x+b_2y+c_2=0\)　(\(a_2≠0\) または \(b_2≠0\))・・・②
の平行・垂直条件を考えてみます。

(1)\(b_1≠0\) かつ \(b_2≠0\) のとき
この場合は①②どちらも　\(y=mx+n\) の形にできて
①は \(y=-\displaystyle\frac{a_1}{b_1}x-\displaystyle\frac{c_1}{b_1}\)　②は \(y=-\displaystyle\frac{a_2}{b_2}x-\displaystyle\frac{c_2}{b_2}\)
よって
2直線が平行である条件は
\(-\displaystyle\frac{a_1}{b_1}=-\displaystyle\frac{a_2}{b_2}\)　つまり \(a_1b_2-a_2b_1=0\)

2直線が垂直である条件は
\((-\displaystyle\frac{a_1}{b_1})(-\displaystyle\frac{a_2}{b_2})=-1\)　つまり \(a_1a_2+b_1b_2=0\)

(2)\(b_1=0\) のとき
\(a_1≠0\)なので ①は \(x=-\displaystyle\frac{c_1}{a_1}\)　(\(x\)軸に垂直)

2直線が平行であるとき
②も\(x\)軸に垂直な直線となるので、\(b_2=0\),\(a_2≠0\)。 よって\(b_1=b_2=0\) だから(1)で求めた \(a_1b_2-a_2b_1=0\)が成り立ちます。
また、逆に\(a_1b_2-a_2b_1=0\)が成り立つとき、\(b_1=0\) ,\(a_1≠0\)なので\(b_2=0\),さらに\(a_2≠0\)となり、2直線はどちらも\(x\)軸に垂直な直線であり平行となります。

2直線が垂直であるとき
②が\(y\)軸に垂直な直線となるので、\(a_2=0\),\(b_2≠0\)。よって\(b_1=a_2=0\) だから (1)で求めた\(a_1a_2+b_1b_2=0\)が成り立ちます。
また逆に\(a_1a_2+b_1b_2=0\)が成り立つとき、\(b_1=0\), \(a_1≠0\)なので\(a_2=0\),さらに\(b_2≠0\)となり、直線①は\(x\)軸に垂直、直線②は\(y\)軸に垂直であり、2直線は垂直となります。

(3)\(b_2=0\)のとき
(2)と同様に
2直線が平行　\(↔\)　\(a_1b_2-a_2b_1=0\)
2直線が垂直　\(↔\)　\(a_1a_2+b_1b_2=0\)
が成り立ちます。

平行のときはクロスさせて引く、垂直のときは同じ文字の係数どうしを掛けて足すと覚えるとよいでしょう。

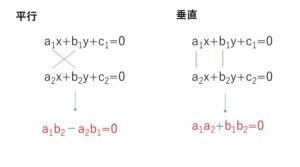
以上のことから \(ax+by+c=0\) に対して
直線\(ax+by+c’=0\) は\(ab-ab=0\)より平行な直線、
直線\(bx-ay+c”=0\) は\(ab+b(-a)=0\)より垂直な直線となります。

(例題1)
点\((-1,2)\)を通り、直線\(3x+2y=5\) に平行・垂直な直線の方程式を求めよ。

(解答)
平行な直線は \(3x+2y+c’=0\)
垂直な直線は \(2x-3y+c”=0\)　と表せる。
それぞれ \((-1,2)\)を通るので
\(-3+4+c’=0\),　\(-2-6+c”=0\)
よって \(c’=-1\),　\(c”=8\)

したがって
平行: \(3x+2y-1=0\)　垂直: \(2x-3y+8=0\)

(例題2)
2直線 \((a-2)x+ay+2=0\),　\(x+(a-2)y+1=0\) が平行となるとき、\(a=\)(ア) であり、特に一致するときは、\(a=\)(イ) である。また垂直となるとき、\(a=\)(ウ) である。

(解答)
平行である条件は
\((a-2)^2-a=0\)
よって \(a^2-5a+4=0\)　 \((a-4)(a-1)=0\)　より
\(a=1,4\)　(ア)

\(a=1\)のとき2直線は
\(-x+1+2=0\),　\(x-y+1=0\) で一致しない。
\(a=4\)のとき2直線は
\(2x+4y+2=0\)　(\(⇔x+2y+1=0\)),　\(x+2y+1=0\) より一致する。
\(a=4\) (イ)

また、垂直である条件は
\((a-2)+a(a-2)=0\)
よって \(a^2-a-2=0\) \((a-2)(a+1)=0\) より
\(a=-1,2\) (ウ)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→点対称・線対称　back→直線の方程式