点対称・線対称の条件についてみていきます。
・点対称・線対称
図より点対称・線対称について次のことが成り立ちます。
2点\(A,B\)が点\(P\)について対称 \(↔\) 線分\(AB\)の中点が\(P\)
・線対称
2点\(A,B\)が直線\(l\)に関して対称
\(↔\)
①線分\(AB\)の中点が\(l\)上にある かつ ②直線\(AB\)と\(l\)は垂直
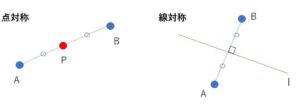
また、線対称に関しては条件は2つです。
どちらかが欠けている場合、例えば①のみのときは次のような図の場合が考えられ、これは線対称ではありません。
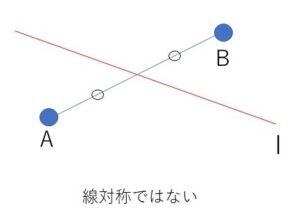
(解説)
(点対称)
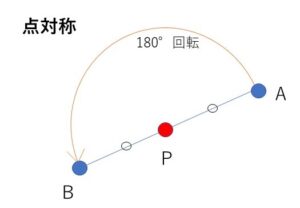
2点\(A,B\)が点\(P\)について対称ということは、\(A\)を\(P\)に関して\(180°\)回転移動させると\(B\)になるということですが、このとき\(AP=BP\)であり、また直線\(AP\)上に\(B\)があるので、\(P\)は\(AB\)の中点となります。
(線対称)
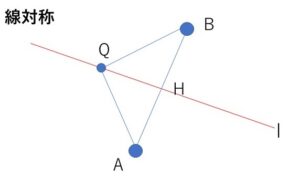
2点\(A,B\)が直線\(l\)に関して対称ということは、\(l\)を軸として平面を折り曲げると、\(A\)と\(B\)が重なるということです。このとき\(AB\)と\(l\)の交点を\(H\)として、\(l\)上に図のように\(Q\)をとり、三角形\(QAB\)を\(l\)を軸にして折り曲げると、\(△QHA\)と\(△QHB\)はぴったり重なり合同となります。
よって、\(AH=BH\) (\(H\)は線分\(AB\)の中点)
また、
\(\angle QHA=\angle QHB\) と \(\angle QHA+\angle QHB=180°\) より
\(\angle QHA=\angle QHB=90°\) (\(AB\)と\(l\)は垂直)
(例題1)
\(P(6,2)\)の 点\((1,1)\)に関する対称点\(Q\)の座標を求めよ。
(解答)
線分\(PQ\)の中点が\((1,1)\)なので、\(Q(x,y)\)とすると
\(\displaystyle\frac{6+x}{2}=1\), \(\displaystyle\frac{2+y}{2}=1\)
よって、\(x=-4\), \(y=0\)
答え \(Q(-4,0)\)
(例題2)
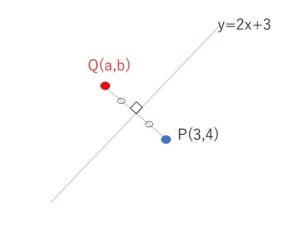
(1)直線 \(y=2x+3\)に関して、点\(P(3,4)\)と対称な点\(Q\)の座標を求めよ。
(2)直線 \(y=2x+3\)に関して、直線 \(3x-2y-1=0\)と対称な直線の方程式を求めよ。
(解答)
(1)
\(Q(a,b)\)とおくと、
①\(PQ\)の中点が\(y=2x+3\)上にある。
②\(PQ\)と\(y=2x+3\)は垂直。
①より \(\displaystyle\frac{4+b}{2}=2・\displaystyle\frac{3+a}{2}+3\)・・・①’
②より \(\displaystyle\frac{b-4}{a-3}・2=-1\)・・・②’
①’②’より
\(a=-1\), \(b=6\)
よって\(Q(-1,6)\)
(2)
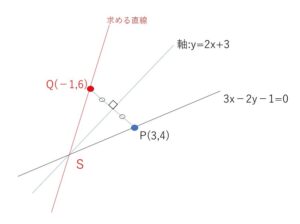
直線は点の集まりなので、直線 \(3x-2y-1=0\)のすべての点において対称軸\(y=2x+3\)に関して対称な点の集まり(直線)が答えとなりますが、それを求めるには(1)を利用します。
まず、点\(P\)は\(3x-2y-1=0\)上の点でなので、求める直線は\(Q\)を通ることになり、また 軸\(y=2x+3\) と \(3x-2y-1=0\)の交点\(S\)について考えると、その交点の線対称な点は自分自身となるので、求める直線は\(S\)と\(Q\)を通る直線となります。
なお、求める直線は1本しか考えられず他に無く、\(SQ\)を通る直線も1つに定まるのでこれが答えとなります。
\(P(3,4)\)は、\(3・3-2・4-1=0\) より \(3x-2y-1=0\)上の点であるので、
求める直線は\(Q(-1,6)\)を通る。
また、\(y=2x+3\) と \(3x-2y-1=0\) の交点\(S\)の座標は \(S(-7,-11)\)であり、求める直線はこの点も通る。
よって\(Q(-1,6)\),\(S(-7,-11)\)を通る直線を求めると
\(y-6=\displaystyle\frac{6+11}{-1+7}(x+1)\)
整理して
\(17x-6y+53=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→線分の垂直二等分線 back→2直線の平行・垂直・一致