交わる2直線の交点を通る直線の表し方について学んでいきます。
(例題)
2直線 \(x+3y-4=0\)・・・① \(2x-y+3=0\)・・・② の交点を\(P\)とする。点\(P\)を通り、直線 \(x-3y=0\) に平行な直線と垂直な直線の方程式を求めよ。
\(x+3y-4+k(2x-y+3)=0\)・・・(※)
と表せることを利用して解いてみます。
(※)が①②の交点\(P\)を通る直線であることの解説
\(x+3y-4+k(2x-y+3)=0\)・・・(※) は
\(x+3y-4=0\) かつ \(2x-y+3=0\) を満たす\((x,y)\)については
\(k\)の値にかからず成り立つので、\(k\)の値によらず①②の交点\(P\)を通る。
また(※)は
\((1+2k)x+(3-k)y\)\(-4+3k\)\(=0\)
であり、\(x,y\)の係数が同時に\(0\)になる\(k\)は存在しないため直線を表し、\(k\)の値を変化させるといろいろな直線を表す。
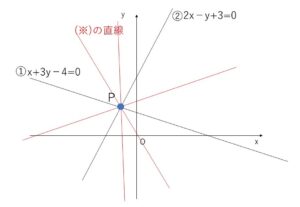
(i)(※)は\(k\)でくくられた部分の 直線② \(2x-y+3=0\) は唯一表さない。(直線①\(x+3y-4=0\)のほうは表す。)
(ii)そもそも交点が存在しない場合は、交点を通る直線を表さない。
(i)については
\(k=0\) とすれば(※)は \(x+3y-4=0\)・・・① となる。
また(※)が \(2x-y+3=0\)を表すと仮定すると
\(x+3y-4+k(2x-y+3)=\)\(2x-y+3\) より
\(x+3y-4=(1-k)(2x-y+3)\)・・・(A)
(A)は \(2x-y+3\)の定数倍が\(x+3y-4\) になることを表しているが、そのような定数は存在しないため矛盾。よって\(2x-y+3=0\)・・・②は表さない。
また、②上にない任意の点を\((s,t)\)とすると
\(2s-t+3≠0\)であり、(※)に\((s,t)\)を代入すると
\(s+3t-4+k(2s-t+3)=0\) より \(k\)が決まり、この\(k\)の値のとき(※)は点Pと点\((s,t)\)を通る直線となる。
よって(※)は②以外の①②の交点を通る直線すべてを表す。
(ii)については例えば交点がない平行な2直線
\(x+2y-1=0\), \(x+2y-4=0\) について
\(x+2y-1+k(x+2y-4)=0\) を考えると、例えば\(k=1\)として
\(2x+4y-5=0\) は直線を表しますがもちろん交点を通る直線ではありません。
長くなったのでもう1度例題を書いて解いてみます。
(例題)
2直線 \(x+3y-4=0\)・・・① \(2x-y+3=0\)・・・② の交点を\(P\)とする。点\(P\)を通り、直線 \(x-3y=0\) に平行な直線と垂直な直線の方程式を求めよ。
(解答)
①②の交点\(P\)を通る直線は
\(x+3y-4+k(2x-y+3)=0\)・・・(※) と表される。整理して
\((1+2k)x+(3-k)y\)\(-4+3k\)\(=0\)・・・③
③が\(x-3y=0\) に平行なとき
\((1+2k)(-3)-1・(3-k)=0\)
よって \(k=-\displaystyle\frac{6}{5}\)
③に代入して
\((1-2・\displaystyle\frac{6}{5})x+(3+\displaystyle\frac{6}{5})y\)\(-4-3・\displaystyle\frac{6}{5}\)\(=0\)
整理すると
\(7x-21y+38=0\) (平行な直線)
③が\(x-3y=0\) に垂直なとき
\((1+2k)・1+(3-k)(-3)=0\)
よって \(k=\displaystyle\frac{8}{5}\)
③に代入して
\((1+2・\displaystyle\frac{8}{5})x+(3-\displaystyle\frac{8}{5})y\)\(-4+3・\displaystyle\frac{8}{5}\)\(=0\)
整理して
\(21x+7y+4=0\) (垂直な直線)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→定点を通る直線 back→2直線の方程式を表す条件