2円の共通接線に関する問題について見ていきます。
(例題)
2つの円
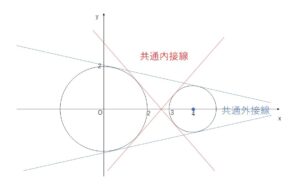
\(C_1:x^2+y^2=4\), \(C_2:(x-4)^2+y^2=1\) の両方に接する直線の方程式を求めよ。
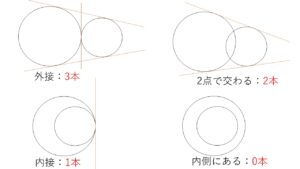
なお図示すると分かりますが、2円は離れているので共通接線は全部で4本あります。
(解答)
\(C_1:x^2+y^2=4\) 上の接点の座標を\((s,t)\)とおくと
\(s^2+t^2=4\)・・・①
またこの点における接線の方程式は
\(sx+ty=4\)・・・②
②が \(C_2:(x-4)^2+y^2=1\) に接するので、直線② \(sx+ty-4=0\) と\(C_2\)の中心\((4,0)\)の距離が半径\(1\)となる。よって
\(\displaystyle\frac{|4s-4|}{\sqrt{s^2+t^2}}=1\)
①より
\(|s-1|=\displaystyle\frac{1}{2}\)
\(s-1=±\displaystyle\frac{1}{2}\) だから
\(s=\displaystyle\frac{3}{2},\displaystyle\frac{1}{2}\)
①より
\(s=\displaystyle\frac{3}{2}\)のとき、\(t=±\displaystyle\frac{\sqrt{7}}{2}\)
\(s=\displaystyle\frac{1}{2}\)のとき、\(t=±\displaystyle\frac{\sqrt{15}}{2}\)
したがって②より接線の方程式は
\(\displaystyle\frac{3}{2}x±\displaystyle\frac{\sqrt{7}}{2}y=4\), \(\displaystyle\frac{1}{2}x±\displaystyle\frac{\sqrt{15}}{2}y=4\)
両辺2倍して
\(3x±\sqrt{7}y=8\), \(x±\sqrt{15}y=8\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2円の交点を通る直線・円 back→2円の位置関係