2円の位置関係について見ていきます。
ポイントは2円の半径と、2円の中心間距離です。
・2円の位置関係
半径の大きさが異なる2円の位置関係は次の場合に分けられます。
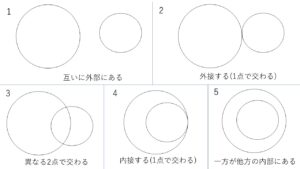
「交わらない(外部にある)→接する(外接)→2点で交わる→接する(内接)→交わらない(内部にある)」
と位置関係が変わるのが分かると思います。
ここで、2円の半径を\(r,r’\) (\(r>r’\))、2円の中心間の距離を\(d\)として、
これらの位置関係を \(r,r\)と\(d\)に関する数式で表していきます。
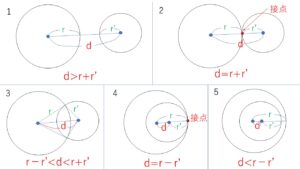
図より
(1)互いに外部にある 「\(d>r+r’\)」
(2)外接する 「\(d=r+r’\)」
(3)異なる2点で交わる 「\(r-r'<d<r+r’\)」
(4)内接する 「\(d=r-r’\)」
(5)一方(大きい方)が他方の内部にある 「\(d<r-r’\)」
となることが分かります。
(3)のときは中心2個と交点1個を結ぶ三角形ができるときで、3辺\(d,r,r’\)の三角形ができる条件と考えてもよいです。
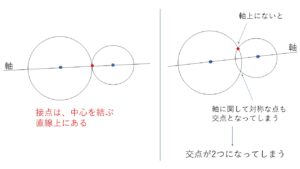
「円は直径を軸として対称な図形なので、2つの円からできた全体の図形は2円の中心を結ぶ直線を軸として対称です。ここでもし、この軸上に交点(接点)がないと仮定すると、軸をはさんで反対側にも交点が存在することになってしまい、1点で交わらなくなってしまってしまうからです。」
内接するときも同様の理由で、中心を結ぶ直線上に接点があります。
また、\(r<r’\)のときは
(3)~(5)の \(r-r’\) の部分が \(r’-r\) に変わるだけで
\(\begin{eqnarray}
|r-r’|
=
\begin{cases}
r-r’ & (r>r’) \\
r’-r & (r<r’)
\end{cases}
\end{eqnarray}\)
より、半径の大きさが異なる2円について次のようにまとめることができます。
(1)互いに外部にある 「\(d>r+r’\)」
(2)外接する 「\(d=r+r’\)」
(3)異なる2点で交わる 「\(|r-r’|<d<r+r’\)」
(4)内接する 「\(d=|r-r’|\)」
(5)一方(大きい方)が他方の内部にある 「\(d<|r-r’|\)」
なお、2円の半径の大きさが同じ場合には
(1)~(3)までは同様で、(4)のときは2円がぴったり重なり(一致し)、(5)の場合はありえません。
(例題1)
2つの円
\(x^2+y^2+2x+6y+6=0\)・・・①
\(x^2+y^2+10x+12y+4k=0\)・・・②
が共有点をもつように、定数\(k\)の値の範囲を求めよ。
共有点をもつ場合は、(2)外接(3)異なる2点で交わる(4)内接 の場合です。
(解答)
①は \((x+1)^2+(y+3)^2=4\)
②は \((x+5)^2+(y+6)^2=-4k+61\) (ただし\(k<\displaystyle\frac{61}{4}\))
中心間の距離は、\(\sqrt{4^2+3^2}=5\) なので
①②が共有点をもつ場合は、
\(|2-\sqrt{-4k+61}|≦5≦2+\sqrt{-4k+61}\)・・・③
③の左辺と中辺については
\(-5≦2-\sqrt{-4k+61}≦5\) より
\(-3≦\sqrt{-4k+61}≦7\)
③の中辺と右辺は
\(3≦\sqrt{-4k+61}\) なので
\(3≦\sqrt{-4k+61}≦7\)
全ての辺は\(0\)以上の値なので
\(9≦-4k+61≦49\)
したがって
\(3≦k≦13\) (\(k<\displaystyle\frac{61}{4}\)を満たす)
(例題2)
円\(O:(x+2)^2+(y-4)^2=20\) と原点において外接する、半径\(\sqrt{5}\)である円の方程式を求めよ。
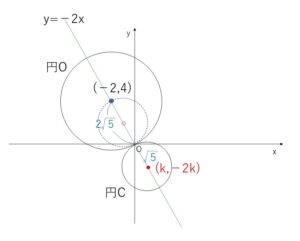
円\(O\)と求める円\(C\)は原点で外接しているので、円\(C\)の中心は円\(O\)の中心\((-2,4)\)と原点\((0,0)\)を結ぶ直線 \(y=-2x\) 上にある。
よって円\(C\)の中心を \((k,-2k)\)とおくと、円\(C\)は原点を通る半径\(\sqrt{5}\)の円より
\(k^2+(-2k)^2=(\sqrt{5})^2\)
これを解くと
\(k=±1\)
\(k=-1\)のときは円\(C\)が円\(O\)の内側にある(内接している)ので不適。
よって\(k=1\) のとき円\(C\)の方程式は、中心\((1,-2)\),半径\(\sqrt{5}\)の円より
\((x-1)^2+(y+2)^2=5\)
(別解)
求める円\(C\)の中心を\((a,b)\)とおく。
2円の半径はそれぞれ \(2\sqrt{5},\sqrt{5}\)なので、2円の中心 \((a,b)\),\((-2,4)\)の距離を考えて
\(\sqrt{(a+2)^2+(b-4)^2}=3\sqrt{5}\)・・・①
円\(C\)は原点を通る半径\(\sqrt{5}\)の円だから
\(a^2+b^2=5\)・・・②
①の両辺は\(0\)以上の値より
\((a+2)^2+(b-4)^2=45\)
展開すると
\(a^2+b^2+4a-8b=25\)
②を代入して\(4\)で割ると
\(a-2b=5\)
\(a=2b+5\)・・・③ を②に代入して整理すると
\(b^2+4b+4=0\)
\((b+2)^2=0\)
よって \(b=-2\)
③に代入して \(a=1\)
したがって円\(C\)の方程式は
\((x-1)^2+(y+2)^2=5\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→共通接線 back→弦・接線の長さ