2円の交点を通る直線・円の方程式の表し方について学んでいきます。
考え方は、2直線の交点を通る直線のときと同じです。
(例題)
2つの円 \(x^2+y^2=1\) と \((x-2)^2+(y-1)^2=4\) の交点\(P,Q\)を通る直線の方程式を求めよ。また、2点\(P,Q\)を通る半径\(\sqrt{8}\)の円の中心の座標を求めよ。
\(x^2+y^2-1=0\)・・・(A) , \((x-2)^2+(y-1)^2-4=0\)・・・(B) として、直線どうしの場合と同じように定数\(k\)を用いて
\(k(x^2+y^2-1)\)\(+\{(x-2)^2\)\(+(y-1)^2\)\(-4\}=0\)・・・①
とします。2円の交点を\((s,t)\)とすると、
\(s^2+t^2-1=0\) , \((s-2)^2+(t-1)^2-4=0\) が成り立つので、\(k\)の値よらず①は2円の交点\((s,t)\)を通ります。
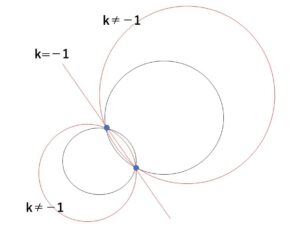
ここで①の\(k\)の値を色々動かすと、\(k=-1\)のときは2次の項が消えるので1次式になり、その他の場合は2次式となります。
1次式のときは2点を通る直線になり、2次式の場合には\(x^2\)と\(y^2\)の係数が同じ2次式となるので2点を通る円となります。・・・(注)詳しくは後述します。
(解答)
定数\(k\)を用いて
\(k(x^2+y^2-1)\)\(+\{(x-2)^2\)\(+(y-1)^2\)\(-4\}=0\)・・・①
とおくと①は2円の交点を通る図形を表す。
ここで\(k=-1\)を代入すると
\(-(x^2+y^2-1)+(x^2-4x+y^2-2y+1)\)\(=0\)
整理すると
\(2x+y-1=0\)・・・②
②は直線を表し2円の2交点を通る。
答 \(2x+y-1=0\)
また、\(k≠-1\)とすると①は
\((k+1)x^2+(k+1)y^2-4x-2y\)\(=k-1\)
両辺\(k+1\)で割って平方完成すると
\((x-\displaystyle\frac{2}{k+1})^2+(y-\displaystyle\frac{1}{k+1})^2\)\(-(\displaystyle\frac{2}{k+1})^2-(\displaystyle\frac{1}{k+1})^2\)\(=\displaystyle\frac{k-1}{k+1}\)
よって
\((x-\displaystyle\frac{2}{k+1})^2+(y-\displaystyle\frac{1}{k+1})^2\)\(=\displaystyle\frac{k^2+4}{(k+1)^2}\)・・・③
③は円を表し、半径が\(\sqrt{8}\)だから
\(\displaystyle\frac{k^2+4}{(k+1)^2}=8\)
整理して
\(7k^2+16k+4=0\)
\((7k+2)(k+2)=\) より
\(k=-\displaystyle\frac{2}{7},-2\)
円の中心は③より \((\displaystyle\frac{2}{k+1},\displaystyle\frac{1}{k+1})\) だから
\(k=-\displaystyle\frac{2}{7}\) のとき \((\displaystyle\frac{14}{5},\displaystyle\frac{7}{5})\)
\(k=-2\) のとき \((-2,-1)\)
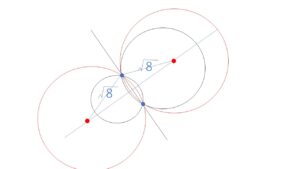
よってこの線分を挟んで両側に半径\(\sqrt{8}\)の円ができます。
今まで直線どうしの交点を通る図形、円どうしの交点を通る図形について考えてきましたが、一般論として次のことが成り立ちます。
方程式 \(kf(x,y)+g(x,y)=0\)・・・(※)
はそれらの交点をすべて通る図形を表す。(ただし\(f(x,y)=0\)は表さない)
(解説)
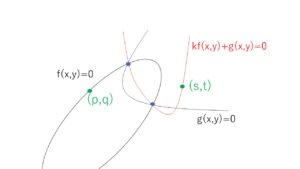
2曲線の交点を\(n\)個として、それぞれを\((x_k,y_k)\) (\(k=1,2,・・・n\)) とする。2曲線はこれらの点を通るから
\(f(x_k,y_k)=0\), \(g(x_k,y_k)=0\)
よって (※)は\((x_k,y_k)\)を通る図形となる。
また、2曲線の交点以外の\(f(x,y)\)上に無い任意の点を \((s,t)\)とおく。
(※)がこの\((s,t)\)を通るとき
\(kf(s,t)+g(s,t)=0\)
\(f(s,t)≠0\) だから
\(k=-\displaystyle\frac{g(s,t)}{f(s,t)}\) となる\(k\)が存在するため、(※)は交点と交点以外の任意の\((s,t)\)(\(f(x,y)=0\)上にはない点)を通る図形となる。
ここで、\(f(x,y)=0\)上の交点\((x_k,y_k)\)以外の点を\((p,q)\)とおく。
(※)に\((p,q)\)を代入すると
\(kf(p,q)+g(p,q)=0\)・・・(A)
\(f(p,q)=0\),\((p,q)\)は交点以外の\(f(x,y)=0\)上の点なので\(g(p,q)≠0\)。
よって(A)を満たす\(k\)は存在しない。
したがって(※)は交点とそれ以外の\(f(x,y)=0\)上を通る図形は表さない。
2曲線がそもそも交点をもたない場合には、\(kf(x,y)+g(x,y)=0\) は交点を通る図形にはもちろんなりません。
(例)交わらない2円
\(f(x,y)=x^2+y^2-1=0\)
\(g(x,y)=(x-6)^2+y^2-1=0\) について
\(k=-1\) として計算すると
\(x=3\) (直線)となりますが、もちろん交点を通る直線ではありません。
では具体的に2曲線が
(ア)ともに直線(1点で交わる) (イ)ともに円(2点で交わる) のときについて考えてみます。
(ア)1点で交わる2直線
\(a_1x+b_1y+c_1=0\), \(a_2x+b_2y+c_2=0\) について
方程式 \(k(a_1x+b_1y+c_1)+a_2x\)\(+b_2y+c_2\)\(=0\)・・・① は
交点を通る1次式で表される図形なので、交点を通る直線を表します。
(仮に\(x,y\)の両方の係数が\(0\)とすると、\(a_1:b_1=a_2:b_2\)となりこれは2直線が平行(一致)するときなので交点が1つであることに矛盾します)
また、①は\(a_1x+b_1y+c_1=0\)は表しません。
(イ)2点で交わる2円
\(x^2+y^2+l_1x+m_1y+n_1\)\(=0\)
\(x^2+y^2+l_2x+m_2y+n_2\)\(=0\) について
方程式
\(k(x^2+y^2+l_1x+m_1y+n_1)\)\(+x^2+y^2+l_2x\)\(+m_2y+n_2\)\(=0\)・・・② は、
\(k=-1\) のとき 1次式となるので2交点を通る直線を表します。
(もし\(x,y\)の係数がどちらも\(0\)だとすると、\(l_1=l_2\),\(m_1=m_2\) ですが、このとき2円の中心が同じになってしますので2交点を通ることと矛盾します)
\(k≠-1\)のときは \(x^2,y^2\)の係数が同じである2次式となるので、2交点を通る円を表します。
(もし②を平方完成して定数部分を右辺に移項したとき、(右辺)\(≦0\)とすると②が2(交)点を通ることと矛盾するので、(右辺)\(>0\)。よって円を表します)
また②は \(x^2+y^2+l_1x+m_1y+n_1\)\(=0\) は表しません。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円と直線の交点を通る円 back→共通接線