円の接点が与えられている場合(もしくは設定した場合)の、円の接線の方程式について学んでいきます。
・円の接線の方程式(原点が中心)
まずは原点を中心とする円から始めます。
円 \(x^2+y^2=r^2\) 上の点\(P\)\((x_1,y_1)\) におけるこの円の接線\(l\)について求めてみます。
「\(OP\)の傾きを求める→\(OP\)に垂直な接線の傾きが分かる→\((x_1,y_1)\)を通るから接線の方程式が求まる」
接線と直線\(OP\)のどちらも傾きが存在するように、どちらの直線も\(x\)軸に垂直にならない場合から考えます。このとき接点は\(x,y\)軸上にないことになります。(\((±r,0)\),\((0,±r)\)の4点以外にある)
傾きの式の分母が\(0\)にならないように場合分けすると考えてもよいです。
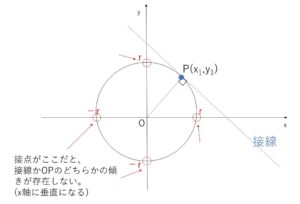
(1)点\(P\)が座標軸上にないとき (\(x_1≠0\) かつ \(y_1≠0\))
図より、\(OP\)の傾きは \(\displaystyle\frac{y_1}{x_1}\) だから 接線の傾きは \(-\displaystyle\frac{x_1}{y_1}\)
接線は\(P(x_1,y_1)\)を通るから、その方程式は
\(y-y_1=-\displaystyle\frac{x_1}{y_1}(x-x_1)\)
整理して
\(x_1x+y_1y=x_1^2+y_1^2\)
また、\((x_1,y_1)\)は円上にあるので、\(x_1^2+y_1^2=r^2\)
したがって接線の方程式は
\(x_1x+y_1y=r^2\)・・・①
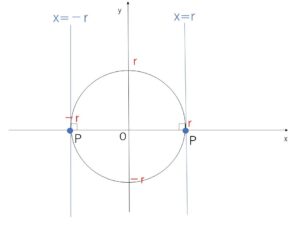
(2)点\(P\)が\(x\)軸上にあるとき (\(y_1=0\))
点\(P\)は \((x_1,y_1)\)\(=(r,0),(-r,0)\)であり、このとき接線は図よりそれぞれ\(x\)軸に垂直な直線
\(x=r\), \(x=-r\)・・・②
②の式は ①で \(x_1=r\), \(y_1=0\) または \(x_1=-r\), \(y_1=0\)
とおくと得られるので、この場合も接線の方程式は①で表されます。
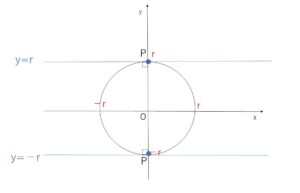
(3)点\(P\)が\(y\)軸上にあるとき (\(x_1=0\))
点\(P\)は \((x_1,y_1)\)\(=(0,r),(0,-r)\)であり、このとき接線は図よりそれぞれ\(x\)軸に平行な直線
\(y=r\), \(y=-r\)・・・③
③の式は ①で \(x_1=0\), \(y_1=r\) または \(x_1=0\), \(y_1=-r\)
とおくと得られるので、この場合も接線の方程式は①で表されます。
以上から接線の方程式は点\(P\)の位置に関係なく
\(x_1x+y_1y=r^2\)
\(x_1x+y_1y=r^2\)
なお今考えた接点における接線の方程式も重要ですが、
・円と直線の式から1文字消去した2次式の判別式 \(D=0\)
・円の半径\(r\)=円の中心と直線の距離\(d\)
の考え方も大事なのでこちらも押さえておきましょう。
・円の接線の方程式(中心が\((a,b)\))
中心が原点の円の接線の方程式を利用できるように、図形全体を円の中心が原点にくるように平行移動させます。すなわち
円\(C:(x-a)^2+(y-b)^2=r^2\) と \(C\)上の点\(P(x_2,y_2)\)の接線について
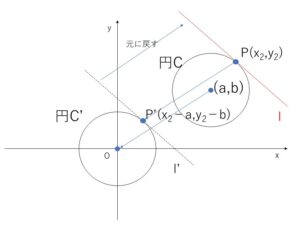
円\(C\)の中心は \((a,b)\)なので、\(x\)軸方向に\(-a\)、\(y\)軸方向に\(-b\) だけ平行移動させると
円\(C\) → 円\(C’:x^2+y^2=r^2\)
点\(P\) → 点\(P'(x_2-a,y_2-b)\)
接線\(l\) → 接線\(l’\)
よって移動後の接線\(l’\)の方程式は、原点中心の円\(C’\)の点\(P’\)における接線で
\(l’:(x_2-a)x+(y_2-b)y=r^2\)
最後に全体の図形を元に戻します。
もとの接線\(l\)は、\(l’\)を\(x\)軸方向に\(a\)、\(y\)軸方向に\(b\)平行移動させた直線なので
\(l:(x_2-a)(x-a)+(y_2-b)(y-b)=r^2\)
\((x-a)(x-a)+(y-b)(y-b)=r^2\) とみて、片方の\(x→x_2\),\(y→y_2\) と置き換えたものになっています。
(例題)
(1)円 \(x^2+y^2=8\) 上の点\((2,-2)\) における接線の方程式を求めよ。
(2)円 \(x^2+y^2-2x-4y-20=0\) 上の点 \((4,6)\) における接線の方程式を求めよ。
(解答)
(1)
接線の方程式は
\(2x-2y=8\) より \(x-y=4\)
(2)
\(x^2+y^2-2x-4y-20=0\) より
\((x-1)^2+(y-2)^2-1-4-20=0\)
\((x-1)^2+(y-2)^2=25\)
この円上の点 \((4,6)\)における接線は
\((4-1)(x-1)+(6-2)(y-2)=25\)
\(3(x-1)+4(y-2)=25\) だから整理して
\(3x+4y=36\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線の方程式② back→円と直線の位置関係