円の接線に関する問題について見ていきます。
(例題1)
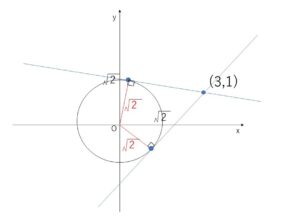
点\((3,1)\)を通り、円\(x^2+y^2=2\) に接する直線の方程式を求めよ。
・円の中心と直線の距離\(d\)\(=\)半径\(r\)
・円と直線の式から1文字消去した2次式の \(D=0\)
・接点による公式
などを利用します。
なお、図を描いても、円の方程式に\((3,1)\)を代入しても分かりますが、\((3,1)\)は円上にないので、接点による公式を利用する場合には接点の座標を設定する必要があります。
(解答1)\(d=r\)を利用
求める接線の方程式は\(x\)軸に垂直な直線 \(x=3\)ではないので
\(y-1=m(x-3)\)・・・① とおける。
この円の接線で、\(x\)軸に垂直となるものは \(x=±\sqrt{2}\) の2本より、\(x=3\)でないと考えてもよいです。
①\(mx-y-3m+1=0\) と 円 \(x^2+y^2=2\) の中心 \((0,0)\) の距離が半径となるので
\(\displaystyle\frac{|-3m+1|}{\sqrt{m^2+1}}\)\(=\sqrt{2}\)
\(\sqrt{m^2+1}≠0\) より
\(|-3m+1|=\sqrt{2(m^2+1)}\)
両辺\(0\)以上の値なので2乗して整理すると
\(7m^2-6m-1=0\)
\((7m+1)(m-1)=0\) より
\(m=-\displaystyle\frac{1}{7},1\)
したがって①より 接線の方程式は
\(y=-\displaystyle\frac{1}{7}x+\displaystyle\frac{10}{7}\)
\(y=x-2\)
(解答2)\(D=0\)の利用
接線は\(x=3\)でないので、接線を \(y-1=m(x-3)\)・・・① とおく。
①より \(y=mx-3m+1\)
\(x^2+y^2=2\)・・・② に代入して
\(x^2+(mx-3m+1)^2=2\)
整理すると
\((m^2+1)x^2+2m(-3m+1)x\)\(+(-3m+1)^2-2\)\(=0\)・・・③
①と②が接するとき \(x\)の2次方程式③は重解をもつので
\(\displaystyle\frac{D}{4}=0\)
\(m^2(-3m+1)^2-(m^2+1)\{(-3m+1)^2-2\}\)\(=0\)
\((-1)(-3m+1)^2\) と \(-(m^2+1)(-2)\) です。
\(-(-3m+1)^2+2(m^2+1)=0\)
整理して
\(7m^2-6m-1=0\)
(※以下解答1と同様です)
\((7m+1)(m-1)=0\) より
\(m=-\displaystyle\frac{1}{7},1\)
したがって①より 接線の方程式は
\(y=-\displaystyle\frac{1}{7}x+\displaystyle\frac{10}{7}\)
\(y=x-2\)
\(x=\displaystyle\frac{m(3m-1)}{m^2+1}\)
となり、\(m=-\displaystyle\frac{1}{7},1\)を代入すると\(x\)座標が出て、あとはこの\(x\)を接線の方程式に代入すれば\(y\)座標も出ます。
(解答3)接点の公式の利用
接点を\((s,t)\)とおくと、接線の方程式は
\(sx+ty=2\)
これが\((3,1)\)を通るので
\(3s+t=2\)・・・(A)
また \((s,t)\)は 円\(x^2+y^2=2\) 上の点だから
\(s^2+t^2=2\)・・・(B)
(A)より \(t=-3s+2\)・・・(C) を(B)に代入して
\(s^2+(-3s+2)^2=2\)
\(10s^2-12s+2=0\)
\(5s^2-6s+1=0\)
\((5s-1)(s-1)=0\)
よって\(s=\displaystyle\frac{1}{5},1\)
(C)より
\(s=\displaystyle\frac{1}{5}\) のとき \(t=\displaystyle\frac{7}{5}\)
\(s=1\) のとき \(t=-1\)
したがって接線は
\(\displaystyle\frac{1}{5}x+\displaystyle\frac{7}{5}y=2\)
\(x-y=2\)
答え \(x+7y=10\), \(x-y=2\)
(例題2)
\(x^2+y^2-2x+4y-5=0\) の接線のうち、傾きが\(3\)となる直線の方程式を求めよ。
(解答1)\(d=r\)の利用
\(x^2+y^2-2x+4y-5=0\) より
\((x-1)^2+(y+2)^2=10\)
これは 中心\((1,-2)\) 半径\(\sqrt{10}\)の円を表す。
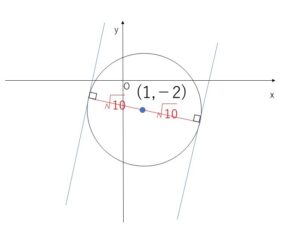
求める接線を \(y=3x+k\) とおくと
\(3x-y+k=0\) と \((1,-2)\)の距離が半径となるので
\(\displaystyle\frac{|3+2+k|}{\sqrt{3^2+1}}\)\(=\sqrt{10}\)
\(|k+5|=10\) より
\(k+5=±10\)
よって \(k=5,-15\)
したがって接線は
\(y=3x+5\), \(y=3x-15\)
(解答2)\(D=0\)の利用
接線を \(y=3x+k\)・・・① とおく。
\(x^2+y^2-2x+4y-5=0\)・・・② に代入して
\(x^2+(3x+k)^2-2x+4(3x+k)-5=0\)
整理すると
\(10x^2+2(3k+5)x+k^2+4k-5\)\(=0\)・・・③
①と②が接するとき③は\(x\)の重解をもつので
\(\displaystyle\frac{D}{4}=0\)
\((3k+5)^2-10(k^2+4k-5)\)\(=0\)
整理して
\(k^2+10k-75=0\)
\((k-5)(k+15)=0\) より
\(k=5,-15\)
したがって接線の方程式は
\(y=3x+5\), \(y=3x-15\)
(解答3)接点の公式の利用
\(x^2+y^2-2x+4y-5=0\) より
\((x-1)^2+(y+2)^2=10\)
接点を\((s,t)\)とおくと、接線の方程式は
\((s-1)(x-1)+(t+2)(y+2)=10\)
傾きが\(3\)なので\(t+2≠0\)。\(y=・・・\)の形にすると
\(y=\displaystyle\frac{1-s}{t+2}(x-1)\)\(+\displaystyle\frac{10}{t+2}-2\)・・・(A)
傾きが\(3\)より \(\displaystyle\frac{1-s}{t+2}=3\)
整理して \(s=-3t-5\)・・・(B)
また \((s,t)\)は円上の点なので
\((s-1)^2+(t+2)^2=10\) ・・・(C)
(B)を(C)に代入して
\((-3t-5-1)^2+(t+2)^2=10\)
展開して整理すると
\(t^2+4t+3=0\)
\((t+1)(t+3)=0\) より
\(t=-1,-3\)
(B)より
\(t=-1\) のとき \(s=-2\)
\(t=-3\) のとき \(s=4\)
よって(A)より接線の方程式は
\(y=3(x-1)+10-2\), \(y=3(x-1)-10-2\)
したがって
\(y=3x+5\), \(y=3x-15\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の接線の方程式③ back→円の接線の方程式①