関数\(f(x)\)や曲線を対称移動させたとき、どのような方程式に変わるか考えていきます。
→(2-1)グラフの平行移動 →(2-2)グラフの対称移動 (2次関数のところで扱っています) を参照してください。
(例題1)
直線 \(y=-1\) に関して 放物線 \(y=x^2-4x+1\) と対称な曲線の方程式を求めよ。
まずは、放物線\(y=f(x)\)上の点 \(P(t,f(t))\) と対称な点を \(Q(X,Y)\) とおいて、\(X,Y\)の方程式を求める方法です(軌跡による解法)。
(解法1)軌跡による解法
放物線\(y=f(x)=x^2-4x+1\) 上の点 \(P(t,f(t))\) と対称な点を\(Q(X,Y)\)とおく。
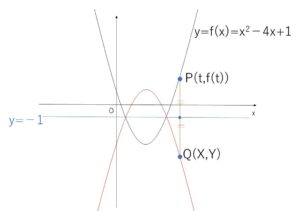
\(y=-1\)に関して対称なので図より
\(X=t\)・・・① (\(x\)座標は同じ)
\(\displaystyle\frac{f(t)+Y}{2}=-1\)・・・② (中点が\(y=-1\)上にある)
②より
\(Y=\)\(-f(t)-2\)\(=-t^2+4t-3\)・・・③
①③より
\(Y=-X^2+4X-3\)
答 放物線 \(y=-x^2+4x-3\)
(解法2)\(x\)軸についての対称移動を利用する方法
よって 対称軸 \(y=-1\) と \(y=x^2-4x+1\) を軸が\(x\)軸に重なるように平行移動させます。そしてこれを\(x\)軸について対称移動させて、最後に元に戻すように平行移動させます。
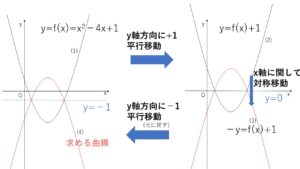
\(y=f(x)=x^2-4x+1\)・・・(1) と対称軸 \(y=-1\) を\(y\)軸方向に1だけ平行移動させると
放物線:\(y=f(x)+1\)・・・(2) 対称軸:\(y=0\) (\(x\)軸)
これを\(x\)軸に関して対称移動すると
放物線: \(-y=f(x)+1\) つまり \(y=-f(x)-1\)・・・(3)
\(y\)軸方向に \(-1\)だけ平行移動させて戻すと
放物線: \(y=-f(x)-2\)・・・(4)
よって求める曲線の方程式は
\(y\)\(=-(x^2-4x+1)-2\)\(=-x^2+4x-3\)
次は点対称に関する問題です。
(例題2)
関数 \(y=f(x)\) を 点\((p,q)\)に関して対称移動させた曲線の方程式は、
\(y=-f(2p-x)+2q\) となることを示せ。
(解法1)軌跡による解法
\(y=f(x)\) 上の 点\(P(t,f(t))\) の対称点を\(Q(X,Y)\) とおく。
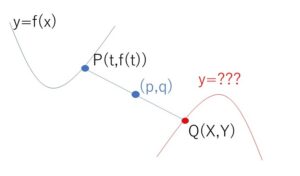
\((p,q)\)について対称なので
\(\displaystyle\frac{t+X}{2}=p\)・・・①
\(\displaystyle\frac{f(t)+Y}{2}=q\)・・・②
①②より
\(X=2p-t\)・・・③
\(Y=2q-f(t)\)・・・④
③④より\(t\)を消去する。
③より \(t=2p-X\) ④に代入して
\(Y=-f(2p-X)+2q\)
よって対称移動後の曲線の方程式は
\(y=-f(2p-x)+2q\)
(解法2)原点に関する対称移動を利用する方法
そしてそのグラフを原点について対称移動させて、最後に元に戻します。
なお原点について対称移動すると、\(x→-x\), \(y→-y\) と変化します。
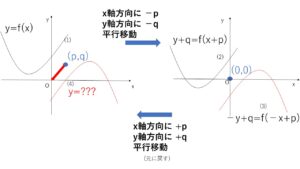
\(y=f(x)\)・・・(1)のグラフを \((p,q)\)が原点にくるように、\(x\)軸方向に\(-p\),\(y\)軸方向に\(-q\)だけ平行移動させる。移動後のグラフの方程式は
\(y+q=f(x+p)\) より \(y=f(x+p)-q\)・・・(2)
次に原点について対称移動させると
\(-y=f(-x+p)-q\) より \(y=-f(-\)\(x\)\(+p)+q\)・・・(3)
最後に \(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ平行移動させて戻すと
\(y-q=-f(-\)\((x-p)\)\(+p)+q\)・・・(注) より
\(y=-f(2p-x)+2q\)・・・(4)
(4)が求める対称移動後の曲線の方程式となる。
(3)→(4)のところは \(x\)軸方向に\(+p\)平行移動するので、\(x→x-p\) と変換するから、\(f(-(x-p)+p)\)となります。\(f(-x-p+p)\)ではありません。
(例題3)
直線 \(x-y+1=0\) に関して、曲線 \(x^2+y^2-x+2y=0\) と対称な曲線の方程式を求めよ。
\((x-\displaystyle\frac{1}{2})^2+(y+1)^2=\displaystyle\frac{5}{4}\) より円です。これを直線に関して対称移動させても円で、大きさ(半径)も変わりません。なので、中心の位置がどう変わるかだけに着目します。
(解答)
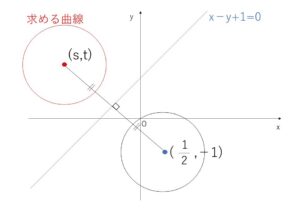
曲線 \(x^2+y^2-x+2y=0\) を変形すると
\((x-\displaystyle\frac{1}{2})^2+(y+1)^2=\displaystyle\frac{5}{4}\)
これは円であり、この円と直線 \(x-y+1=0\) に関して対称な曲線は半径が同じ大きさの円である。
中心 \((\displaystyle\frac{1}{2},-1)\) の対称点を \((s,t)\)とおくと、\((s,t)\)は求める円の中心であり次のことが成り立つ。
\(\displaystyle\frac{s+\displaystyle\frac{1}{2}}{2}-\displaystyle\frac{t-1}{2}+1=0\)・・・① (2円の中心の中点が \(x-y+1=0\) 上にある)
\(\displaystyle\frac{t+1}{s-\displaystyle\frac{1}{2}}・1=-1\)・・・② (中心どうしを結ぶ直線と \(x-y+1=0\)は垂直)
①より \(s-t=-\displaystyle\frac{7}{2}\)
②より \(s+t=-\displaystyle\frac{1}{2}\)
よって \(s=-2\), \(t=\displaystyle\frac{3}{2}\)
したがって求める曲線(円)の方程式は
\((x+2)^2+(y-\displaystyle\frac{3}{2})^2=\displaystyle\frac{5}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→不等式の表す領域①(基礎) back→2接線の交点の軌跡