媒介変数と軌跡 | 教えて数学理科

媒介変数に関する軌跡の問題について見ていきます。

(例題1)
実数\(a\)に対して、曲線 \(C:x^2+3ax+y^2+(a-4)y\)\(-7a-1\)\(=0\) を考える。曲線\(C\)は\(a\)の値にかかわらず円を表すことを示し、円\(C\)の中心を\(P\)とするとき、\(a\)がすべての実数をとるときの点\(P\)の軌跡を求めよ。

まず円であることを示すために平方完成します。

(解答)
曲線\(C\)は
\((x+\displaystyle\frac{3a}{2})^2+(y+\displaystyle\frac{a-4}{2})^2\)\(=(\displaystyle\frac{3a}{2})^2\)\(+(\displaystyle\frac{a-4}{2})^2\)\(+7a+1\)
整理して
\((x+\displaystyle\frac{3a}{2})^2+(y+\displaystyle\frac{a-4}{2})^2\)\(=\displaystyle\frac{5a^2+10a+10}{2}\)・・・①

ここで、
\(5a^2+10a+10\)\(=5(a+1)^2+5\)\(>0\) より
①は中心 \(P(-\displaystyle\frac{3a}{2},-\displaystyle\frac{a-4}{2})\)・・・②の円を表す。

次に円の中心\(P\)の軌跡を求めます。\(P(x,y)\)とおくと②より
\(x=-\displaystyle\frac{3a}{2}\), \(y=-\displaystyle\frac{a-4}{2}\)
です。この2式から\(x,y\)の方程式を導くために、\(a\)を消去します。

また②より\(P(x,y)\)とおくと
\(x=-\displaystyle\frac{3a}{2}\)・・・③
\(y=-\displaystyle\frac{a-4}{2}\)・・・④

③より
\(a=-\displaystyle\frac{2}{3}x\)
④に代入して
\(2y=\displaystyle\frac{2}{3}x+4\)
よって
\(y=\displaystyle\frac{1}{3}x+2\)

答　直線 \(y=\displaystyle\frac{1}{3}x+2\)

\(a\)はすべての実数値をとるので、\(x=-\displaystyle\frac{3a}{2}\)・・・③ より \(x\)もすべての実数値をとり、除外点はありません。

この問題のように、\(x,y\)がある文字\(a\)で表されている場合、この文字\(a\)を媒介変数とよびます。関数として表すと、\(x=f(a)\), \(y=g(a)\) の形になっていて、この表し方を媒介変数表示とよび、\(a\)(実数)を1つ決めると、それに対応する実数\(x,y\)が1つ決まるので、\((x,y)\)は座標平面上を動き図形を表すことになります。

(例題2)
放物線 \(y=ax^2+x+1\) について、\(a\)が正の値をとりながら動くとき、この放物線の頂点が描く軌跡を求めよ。

(例題1)と同様に頂点を\(a\)を使って表します。
ただし\(a\)が正の値という条件がついているので、範囲に注意します

(解答)
放物線の方程式は
\(y=a(x+\displaystyle\frac{1}{2a})^2-\displaystyle\frac{1}{4a}+1\)

頂点の座標を \((x,y)\)とおくと
\(x=-\displaystyle\frac{1}{2a}\)・・・②
\(y=-\displaystyle\frac{1}{4a}+1\)・・・③

\(a>0\) なので②より \(x<0\)

また②より \(\displaystyle\frac{1}{2}x=-\displaystyle\frac{1}{4a}\) だから③より
\(y=\displaystyle\frac{1}{2}x+1\)

答え直線 \(y=\displaystyle\frac{1}{2}x+1\) (\(x<0\))

ちなみにですが、\(a\)が\(0\)以外のすべての実数値をとる場合でも、軌跡は \(y=\displaystyle\frac{1}{2}x+1\) 全体にはなりません。
なぜかというと、\(x=-\displaystyle\frac{1}{2a}\)・・・② より、\(a\)の反比例のグラフを考えれば \(x=0\) とはならないことがわかるので、\(x=0\) (このとき\(y=1\)) が除外点となるからです。

最後に少し複雑な媒介変数の文字消去の問題をやってみます。

(例題3)
\(t\)が実数全体の値をとるとき
\(x=\displaystyle\frac{t}{1+t^2}\), \(y=\displaystyle\frac{t^2}{1+t^2}\)
は\(xy\)平面上でどのような曲線を描くか。

\(y=t・\displaystyle\frac{t}{1+t^2}\)\(=tx\) とみると、\(x≠0\)のとき \(t=\displaystyle\frac{y}{x}\) です。\(x=0\) のときは別口に考えます。

(解答)
\(y=t・\displaystyle\frac{t}{1+t^2}\)\(=tx\) より

(1)\(x≠0\)のとき
\(t=\displaystyle\frac{y}{x}\)
\(x=\displaystyle\frac{t}{1+t^2}\) に代入して

\(x\{1+(\displaystyle\frac{y}{x})^2\}=\displaystyle\frac{y}{x}\)
よって
\(x^2+y^2=y\) より
\(x^2+(y-\displaystyle\frac{1}{2})^2=\displaystyle\frac{1}{4}\)・・・①

①で\(x=0\)のとき \(y=0,1\) なので2点 \((0,0),(0,1)\)は除かれる。

(2)\(x=0\) のとき
\(x=\displaystyle\frac{t}{1+t^2}=0\) より \(t=0\)
このとき
\(y=\displaystyle\frac{t^2}{1+t^2}=0\)
よって点\((0,0)\)をとる。

以上から求める曲線は
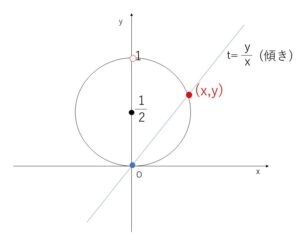
円 \(x^2+(y-\displaystyle\frac{1}{2})^2=\displaystyle\frac{1}{4}\) (\((0,1)\)を除く)

逆の確認ですが、\(x≠0\) のときは \(x\{1+(\displaystyle\frac{y}{x})^2\}=\displaystyle\frac{y}{x}\) までは解答の逆をたどればよく、ここで \(t=\displaystyle\frac{y}{x}\) とおくと、問題文の媒介変数表示が得られます。あとは\(\displaystyle\frac{y}{x}\)が任意の値をとるかですが、\(t=\displaystyle\frac{y}{x}\)は得られた円上の点と原点を結ぶ直線の傾きなので、\(x≠0\) のときは \(0\)以外のすべての値をとります。
また、\(x=0(=y)\) のときは媒介変数表示において\(t=0\)とすればよいので、結局問題文の条件を満たします。

数Ⅲの微分の知識があれば、\(x,y\)について増減表を考えれば、描く図形の除外点や\(t\)を変化させたときの\(x,y\)の動き方がつかみやすいです。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→角の二等分線・線対称な図形　 back→動点に対する軌跡