角の二等分線,線対称な図形

角の二等分線や、線対称な図形の方程式を求める問題について見ていきます。

(例題1)
2つの直線 \(2x+y-3=0\), \(x-2y+1=0\) のなす角の2等分線の方程式を求めよ。

(解法1)

求める軌跡上の点を\((x,y)\)とする解法です。
角の2等分線上の点が2直線から同じ距離にあることを利用します。
なお図より角の2等分線は2本ありますが、この解法だと自動的に2つの直線の方程式が出てきます。
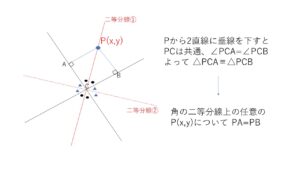解答では直線の方程式に\(x,y\)が使われているので、\(P(X,Y)\)として分かりやすくしてあります。

角の2等分線上の点を\(P(X,Y)\)とおくと、\(P\)が2直線から同じ距離にあるので

\(\displaystyle\frac{|2X+Y-3|}{\sqrt{2^2+1^2}}\)\(=\displaystyle\frac{|X-2Y+1|}{\sqrt{1^2+2^2}}\)
よって
\(|2X+Y-3|=|X-2Y+1|\) より
\(2X+Y-3=±(X-2Y+1)\)

\(2X+Y-3∓(X-2Y+1)=0\) だから
\(X+3Y-4=0\) または \(3X-Y-2=0\)

答 \(x+3y-4=0\), \(3x-y-2=0\)

(解法2)図形的に解く方法

角の2等分線と辺の比の性質を利用して、角の2等分線上のどこか1点を具体的に求めます。
また2等分線は2直線の交点を通るので、求めた点と交点を通る直線が2等分線の方程式となります。もう1本の2等分線の方程式は、2等分線どうしは垂直であることを利用して出します。

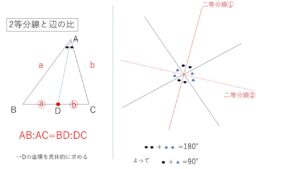
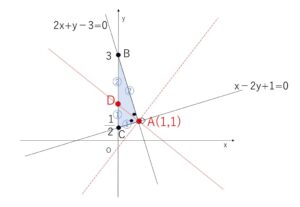
図のように\(A,B,C,D\)を設定する。(\(D\)は\(y\)軸上の角の二等分線上の点)

2直線の交点\(A\)を求めると \(A(1,1)\)
\(AB=\sqrt{2^2+1^2}=\sqrt{5}\)
\(AC=\sqrt{1^2+(\displaystyle\frac{1}{2})^2}=\displaystyle\frac{\sqrt{5}}{2}\)
よって \(AB:AC=2:1\)

\(AD\)は角の二等分線なので、\(BD:DC=2:1\)より
\(D(0,\displaystyle\frac{1\cdot3+2\cdot\displaystyle\frac{1}{2}}{2+1})\)\(=(0,\displaystyle\frac{4}{3})\)

したがって直線\(AD\)の傾きは \(-\displaystyle\frac{1}{3}\)

もう一方の角の二等分線は\(AD\)に垂直なので、その傾きは \(3\)

以上から二等分線の方程式は
\(y-1=-\displaystyle\frac{1}{3}(x-1)\),　\(y-1=3(x-1)\)
整理して
\(x+3y-4=0\),　\(3x-y-2=0\)

(例題2)
直線\(y=2x+3\) に関して 直線 \(3x-2y-1=0\) と対称な直線の方程式を求めよ。

(解答)

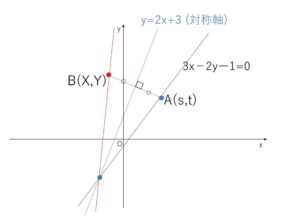
\(3x-2y-1=0\)上の点を\(A(s,t)\)とおくと
\(3s-2t-1=0\)・・・①

また、\(y=2x+3\)に関して 点\(A(s,t)\)と対称な点を\(B(X,Y)\)とおくと
(1)線分\(AB\)の中点が \(y=2x+3\) 上にある。
(2)直線\(AB\)と\(y=2x+3\)が垂直 (ただし\(A,B\)が一致する場合を除く)

(1)より
\(\displaystyle\frac{t+Y}{2}=2・\displaystyle\frac{s+X}{2}+3\)
整理すると
\(2s-t=-2X+Y-6\)・・・②

(2)より
\(A,B\)が一致しないときは \(s≠X\) より
\(\displaystyle\frac{Y-t}{X-s}\cdot2=-1\)
整理すると
\(s+2t=X+2Y\)・・・③
(③は\(A,B\)が一致するとき、つまり\(s=X\), \(t=Y\) のときも成り立つ)

②③より
\(5s=-3X+4Y-12\), 　\(5t=4X+3Y+6\)

①×5  　\(3・5s-2・5t-5=0\) に代入して
\(3(-3X+4Y-12)-2(4X+3Y+6)-5=0\)
整理して
\(17X-6Y+53=0\)

答 \(17x-6y+53=0\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→動く2直線の交点の軌跡　back→媒介変数と軌跡