平面上で \(OP・OQ=\)(一定) の軌跡について見ていきます。
(例題)
座標平面上で原点\(O\)から出る半直線の上に2点\(P,Q\)があり、 \(OP・OQ=2\) を満たしている。
(1)点\(P,Q\)の座標をそれぞれ \((x,y)\),\((X,Y)\) とするとき、\(x,y\)を\(X,Y\)で表せ。
(2)点\(P\)が直線 \(x-3y+2=0\) 上を動くとき、点\(Q\)の軌跡を求めよ。
(3)点\(P\)が円 \((x-1)^2+(y-1)^2=1\) 上を動くとき、点\(Q\)の軌跡を求めよ。
(解答)
(1)
条件より\(k\)を\(X,Y\)であらわすことができれば答えとなります。また、\(OP・OQ=2\)より \(P\)が原点にないので\(k≠0\)。さらに\(O\)に対して同じ側に\(P,Q\)はあるので\(k>0\)です。
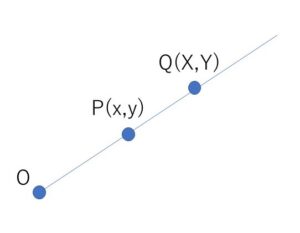
\(P,Q\)が原点\(O\)からでる半直線上にあるので、
\(x=kX\)・・・① \(y=kY\)・・・② とおける。
点\(P\)が原点だと \(OP・OQ=2\) を満たさないので、\(k>0\)
\(OP・OQ=2\) より
\(\sqrt{x^2+y^2}\sqrt{X^2+Y^2}=2\)
①②より
\(\sqrt{k^2(X^2+Y^2)}\sqrt{X^2+Y^2}=2\)
\(k>0\), \(X^2+Y^2≧0\) より
\(k(X^2+Y^2)=2\)
また、\(Q\)も \(OP・OQ=2\) より原点にないので、
\((X,Y)≠(0,0)\)・・・③
よって
\(k=\displaystyle\frac{2}{X^2+Y^2}\)・・・④
④を①②に代入して
\(x=\displaystyle\frac{2X}{X^2+Y^2}\), \(y=\displaystyle\frac{2Y}{X^2+Y^2}\)
\(X=\displaystyle\frac{2x}{x^2+y^2}\), \(Y=\displaystyle\frac{2y}{x^2+y^2}\)
(\(X=k’x\), \(Y=k’y\) とおけば同じように導けます)
(2)
\((X,Y)≠(0,0)\)・・・③ に注意します。
\(x-3y+2=0\) に (1)の結果\(x=\displaystyle\frac{2X}{X^2+Y^2}\), \(y=\displaystyle\frac{2Y}{X^2+Y^2}\) を代入して
\(\displaystyle\frac{2X}{X^2+Y^2}-3・\displaystyle\frac{2Y}{X^2+Y^2}+2\)\(=0\)
両辺 \(X^2+Y^2\)倍して
\(X-3Y+(X^2+Y^2)=0\)
よって
\((X+\displaystyle\frac{1}{2})^2+(Y-\displaystyle\frac{3}{2})^2\)\(=\displaystyle\frac{5}{2}\)・・・⑤
(1)の③より \((X,Y)≠(0,0)\) だから ⑤から原点を除いたものが軌跡となる。
答 円 \((x+\displaystyle\frac{1}{2})^2+(y-\displaystyle\frac{3}{2})^2\)\(=\displaystyle\frac{5}{2}\) (原点を除く)
(3)
\((x-1)^2+(y-1)^2=1\) に(1)の結果\(x=\displaystyle\frac{2X}{X^2+Y^2}\), \(y=\displaystyle\frac{2Y}{X^2+Y^2}\) を代入して
\((\displaystyle\frac{2X}{X^2+Y^2}-1)^2+(\displaystyle\frac{2Y}{X^2+Y^2}-1)^2=1\)
両辺 \((X^2+Y^2)^2\) 倍して
\(\{2X-(X^2+Y^2)\}^2+\{2Y-(X^2+Y^2)\}^2\)\(=(X^2+Y^2)^2\)
\(X^2+Y^2=Z\) とおくと
\((2X-Z)^2+(2Y-Z)^2=Z^2\)
整理して
\(Z^2-4ZX-4ZY+4(X^2+Y^2)=0\)
\(Z^2-4ZX-4ZY+4Z=0\)
\(X≠0\), かつ \(Y≠0\)・・・③より \(Z=X^2+Y^2≠0\) だから \(Z\)で割ると
\(Z-4X-4Y+4=0\)
\(Z\)を \(X,Y\)に戻すと
\(X^2+Y^2-4X-4Y+4=0\)
よって
\((X-2)^2+(Y-2)^2=4\)・・・⑥
⑥は 原点を通らないので \((X,Y)≠(0,0)\)・・・③を満たす。
答 円 \((x-2)^2+(y-2)^2=4\)
※この問題は反転というものを題材にしています。反転やそれに関する軌跡について詳しく見ていきます。
・反転と軌跡
定点\(O\)を中心とする半径\(r(>0)\)(一定)の円がある。\(O\)とは異なる点\(P\)をとり、半直線\(OP\)上に点\(Q\)を \(OP・OQ=r^2\)(一定) となるようにとる。点\(P\)を点\(Q\)に移す変換を反転という。また定点\(O\)を反転の中心、\(r\)を反転の半径という。
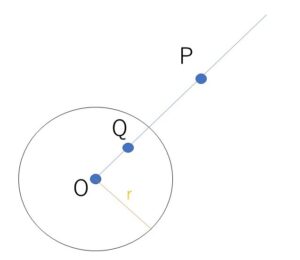
反転について次のことが言えます。
(両方とも同じ側にあると \(OP・OQ=r^2\)(半径の2乗)を満たさない)
・\(P\)が円周上にあれば、反転しても動かない。
・\(P\)を反転させた点\(Q\)を、同じように反転させると\(P\)に戻る。
(\(OP・OQ=\)(一定)のため)
では直線や円を反転させた場合どのような軌跡を描くかについて考えてみます。定点\(O\)を原点として
①原点を通るような直線(原点を除く)
②原点を通るような円(原点を除く)
③原点を通らない直線
④原点を通らない円
の4パターンについて、上の例題のように\(P,Q\)を設定して(1)からの流れに沿ってやってみます。ただし簡単のため \(OP・OQ=1\)とします。なお③④が例題(2)(3)のケースとなっています。
(準備)
\(P(x,y)\),\(Q(X,Y)\) とする。\(k\)を定数として
\(x=kX\)・・・①, \(y=kY\)・・・② とおく。
ただし、\(x,y\)は \(OP・OQ=1\) より \((x,y)≠(0,0)\) だから \(k≠0\)。
また、\(P,Q\)は\(O\)に対して同じ側にあるので \(k>0\)。
\(OP・OQ=1\)より
\(\sqrt{x^2+y^2}\sqrt{X^2+Y^2}=1\)
①②を代入して
\(\sqrt{k^2(X^2+Y^2)}\sqrt{X^2+Y^2}=1\)・・・③
\(Q\)も原点にはないので、\((X,Y)≠(0,0)\)。よって\(X^2+Y^2>0\)
\(k>0\)だから③は
\(k(X^2+Y^2)=1\)
\(k=\displaystyle\frac{1}{X^2+Y^2}\)
①②に代入して
\(x=\displaystyle\frac{X}{X^2+Y^2}\), \(y=\displaystyle\frac{Y}{X^2+Y^2}\) \((X,Y)≠(0,0)\)・・・③
ではこれをもとに、点\(P(x,y)\)が①~④の図形上を動く場合について反転した\(Q(X,Y)\)の軌跡を検討していきます。
①原点を通るような直線(原点を除く)
\(ax+by=0\) を\(P(x,y)\)が動くので ③を代入して
\(\displaystyle\frac{aX}{X^2+Y^2}+\displaystyle\frac{bY}{X^2+Y^2}=0\)
両辺に\(X^2+Y^2\)をかけて
\(aX+bY=0\)・・・ 原点を通るような直線(もとの直線と同じ)
ただし \((X,Y)≠(0,0)\) より原点を除く。
②原点を通るような円(原点を除く)
\((x-a)^2+(y-b)^2=a^2+b^2\) を\(P(x,y)\)が動くので ③を代入して
\((\displaystyle\frac{X}{X^2+Y^2}-a)^2+(\displaystyle\frac{Y}{X^2+Y^2}-b)^2=a^2+b^2\)
\((X^2+Y^2)^2\)を両辺にかけて
\(\{X-a(X^2+Y^2)\}^2+\{Y-b(X^2+Y^2)\}^2\)\(=(a^2+b^2)(X^2+Y^2)^2\)
\(X^2+Y^2=Z\) として 展開整理すると
\(X^2+Y^2-2Z(aX+bY)=0\)
\(Z=X^2+Y^2≠0\)より 両辺これで割って
\(1-2(aX+bY)=0\)
\(2aX+2bY-1=0\)・・・原点を通らない直線
③原点を通らない直線
\(ax+by+c=0\) (\(c≠0\))を\(P(x,y)\)が動くので ③を代入して
\(\displaystyle\frac{aX}{X^2+Y^2}+\displaystyle\frac{bY}{X^2+Y^2}+c=0\)
両辺に\(X^2+Y^2\)をかけて
\(aX+bY+c(X^2+Y^2)=0\)
両辺\(c(≠0)\)で割って、平方完成すると
\((X+\displaystyle\frac{a}{2c})^2+(Y+\displaystyle\frac{b}{2c})^2\)\(=\displaystyle\frac{a^2+b^2}{4c^2}\)・・・(A)原点を通るような円
\(ax+by+c=0\) は直線を表すから\((a,b)≠(0,0)\)で(A)は円を表し、\((X,Y)≠(0,0)\) より原点を除く。よって(A)より軌跡は原点を通るような円(原点を除く)
④原点を通らない円
\((x-a)^2+(y-b)^2=R^2\) (\(R^2≠a^2+b^2\)) を\(P(x,y)\)が動くので ③を代入して
\((\displaystyle\frac{X}{X^2+Y^2}-a)^2+(\displaystyle\frac{Y}{X^2+Y^2}-b)^2=R^2\)
\((X^2+Y^2)^2\)を両辺にかけて
\(\{X-a(X^2+Y^2)\}^2+\{Y-b(X^2+Y^2)\}^2\)\(=R^2(X^2+Y^2)^2\)
\(X^2+Y^2=Z\) として 展開整理すると
\(X^2+Y^2-2ZaX-2ZbY+(a^2+b^2-R^2)Z^2=0\)
\(Z=X^2+Y^2≠0\)より 両辺これで割って
\(1-2aX-2bY+(a^2+b^2-R^2)Z=0\)
見やすくするために \(a^2+b^2-R^2=p(≠0)\) とおいて\(p\)で割ると
\(\displaystyle\frac{1}{p}-\displaystyle\frac{2aX}{p}-\displaystyle\frac{2bY}{p}\)\(+X^2+Y^2\)\(=0\)
平方完成すると
\((X-\displaystyle\frac{a}{p})^2+(Y-\displaystyle\frac{b}{p})^2\)\(=\displaystyle\frac{a^2+b^2-p}{p^2}\)\(=\displaystyle\frac{R^2}{p^2}\)・・・原点を通らない円
(\(R^2≠a^2+b^2\)より\(X=Y=0\)を代入しても方程式が成り立たない)
まとめると
②原点を通るような円(原点を除く)→原点を通らない直線
③原点を通らない直線→原点を通るような円(原点を除く)
④原点を通らない円→原点を通らない円
この記事を書いてから気づいたのですが、②④で展開する際に\((X^2+Y^2)^2\)を掛けるよりも、そのまま展開したほうが楽そうです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2接線の交点の軌跡 back→弦の中点の軌跡