引き続き通過領域に関する問題について見ていきます。
(例題1)
\(xy\)平面上の直線 \(l_t:y=2tx-t^2\) (\(t\)は実数) について
\(t\)が \(|t|≧1\) の範囲を動くとき、直線\(l_t\)が通る点 \((x,y)\) の全体を図示せよ。
(解法1)順像法
\(y=2tx-t^2\) \(|t|≧1\) について
\(x=k\) と固定して\(t\)について整理すると
\(y=-t^2+2kt\)・・・(A)
\(t\)の2次関数(A)について \(t≦-1,t≧1\) での\(y\)の変域を考える。
(A)を平方完成して
\(y=f(t)=-(t-k)^2+k^2\)
\(t≦-1, t≧1\) の範囲で考えるので、軸がどこにあっても\(y\)はいくらでも小さくできるので最小値はなし。よって最大値のみを考えますが、
(1)軸\(k\)について、①\(k≦-1,k≧1\) (\(t\)の範囲に含まれる場合)
と、\(-1<k<1\) のときは2次関数は軸について対称なので、\(-1\)と\(1\)の中間\(0\)を境目にして
(2)軸\(k\)について、②\(-1<k≦0\), ③\(0<k<1\)
で場合分けします。
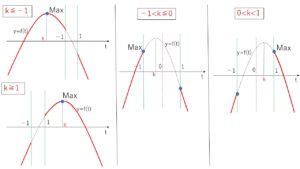
①\(k≦-1,k≧1\) のとき
軸が\(t\)の範囲に含まれるので、\(y=f(t)\)の最大値は \(f(k)=k^2\)
よって \(y≦k^2\)
\(k\)を\(x\)に戻して
\(x≦-1,x≧1\) のとき \(y≦x^2\)
②\(-1<k≦0\) のとき
\(y=f(t)\)の最大値は \(f(-1)=-1-2k\)
よって \(y≦-2k-1\)
\(k\)を\(x\)に戻して
\(-1<x≦0\) のとき \(y≦-2x-1\)
③\(0<k<1\) のとき
\(y=f(t)\)の最大値は \(f(1)=-1+2k\)
よって \(y≦2k-1\)
\(k\)を\(x\)に戻して
\(0<x<1\) のとき \(y≦2x-1\)
以上より①~③を図示すると次の通り。
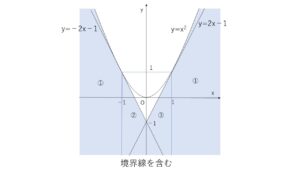
(解法2)逆像法
\(y=2tx-t^2\) より \(t^2-2xt+y=0\)・・・(B)
(B)は\(t\)の2次方程式なので\(|t|≧1\)の範囲で実数解をもつ条件を考えます。なお、2解がともに\(|t|≧1\) の範囲にある必要はなく、1つでもこの範囲にあればよいです。例えば、\((x,y)=(1,0)\) とすると(B)より
\(t^2-2t=0\), \(t=0,2\) となり\(t=0\)は範囲に入っていませんが、\(t=2\)のとき\((1,0)\)を通るので問題ないからです。
\(l_t:y=2tx-t^2\) \(|t|≧1\)
\(t\)について整理すると
\(t^2-2xt+y=0\)・・・(B)
点\((x,y)\)を直線\(l_t\)が通るための条件は、\(t\)の2次方程式(B)が\(t≦-1,t≧1\) の範囲に少なくとも1つの実数解をもつことである。
\(g(t)=t^2-2xt+y\) とおいて
(ア)「2解とも \(t<-1\) の範囲にある」 or 「2解とも \(t>1\) の範囲にある 」(重解を含む)
(イ)「\(t=-1,1\)を解にもつ」
(ウ)「1解が \(t<-1\) もう1解が \(t>-1\)」 or 「1解が \(t>1\) もう1解が \(t<1\)」
\(g(t)=t^2-2xt+y\)\(=(t-x)^2-x^2+y\) とおく。
(ア)2つの実数解をもち、ともに \(t<-1\) の範囲にある または ともに\(t>1\)の範囲にある場合
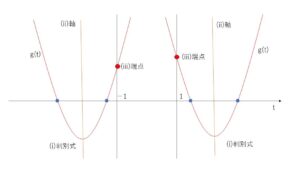
(i)\(D≧0\)
(ii)軸: \(x<-1\)
(iii)端点: \(g(-1)>0\)
または
(i)\(D≧0\)
(ii)軸: \(x>1\)
(iii)端点: \(g(1)>0\)
\(\displaystyle\frac{D}{4}=x^2-y\) より、まとめると
\(x^2-y≧0\), \(x<-1\), \(1+2x+y>0\)
または
\(x^2-y≧0\), \(x>1\), \(1-2x+y>0\)
(イ)\(t=-1,1\)を解にもつとき
\(g(-1)=0\) または \(g(1)=0\) より
\(1+2x+y=0\) または \(1-2x+y=0\)
(ウ)「1解が \(t<-1\) もう1解が \(t>-1\)」 or 「1解が \(t>1\) もう1解が \(t<1\)」のとき
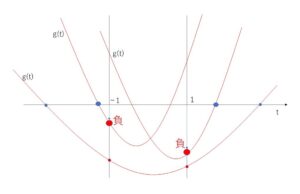
\(g(-1)<0\) または \(g(1)<0\) より
\(1+2x+y<0\) または \(1-2x+y<0\)
以上より領域を図示すると次の通り。
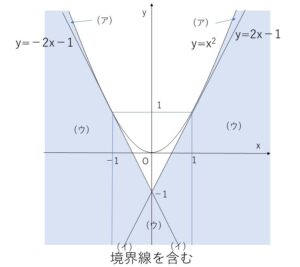
(例題2)
\(xy\)平面上で曲線 \(C:y=\displaystyle\frac{x^2}{4}\) (\(x>0\))上の点\(P\)を中心とし、\(x\)軸に接する円を考える。\(P\)が\(C\)上を動くとき、この円の内部が動く範囲を図示せよ。
(解答)
\(P(t,\displaystyle\frac{t^2}{4})\) (\(t>0\)) とおく。
円の半径は \(P\)の\(y\)座標と等しいので円の内部は次の不等式で表される。
\((x-t)^2+(y-\displaystyle\frac{t^2}{4})^2<(\displaystyle\frac{t^2}{4})^2\)・・・①
順像法で解こうとするには、\(y\)が2次式なので1次の形にするとしても\(y<・・・\), \(y>・・・\)の式が複雑ですし大変そうです。よって逆像法で解いていきたいと思います。
点\((x,y)\)が①を満たすとき(点\((x,y)\)が円の内部にあるとき)それに対応する\(t(>0)\)が存在するので、①を満たす\(t\)の存在条件を考えていきます。
\(t\)の存在条件を考えるため、①を\(t\)について整理します。
①を展開して2倍して\(t\)について整理すると
\((2-y)t^2-4xt+2(x^2+y^2)\)\(<0\)・・・①’
\((x,y)\)が求める範囲に属する点であるための条件は
不等式①’を満たす\(t(>0)\)が存在することである。
\(t^2\)の係数が\(y\)の値によって変わってくるので、「0・負・正」に着目してグラフの形状を考えていきます。
\(f(t)=\)\((2-y)t^2-4xt+2(x^2+y^2)\) とおくと
(ア)\(2-y=0\) のとき (\(y=2\)のとき)
\(f(t)=-4xt+2(x^2+4)\)
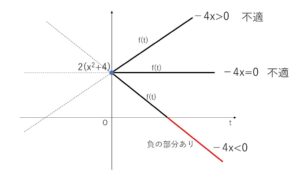
\(f(t)\)は\(t\)の1次関数で、\(y\)切片は \(2(x^2+4)\)\(>0\) で正の値。
したがって、傾き\(-4x\)について
\(-4x=0\), \(-4x>0\) のときは、\(t>0\)の部分で負の値にはならないので不適。
\(-4x<0\) のときは、右下がりのグラフとなり\(f(t)<0\) となる正の数\(t\)が存在する。よって\(x>0\)
まとめると \(y=2\) かつ \(x>0\)
(イ)\(2-y<0\) のとき (\(y>2\)のとき)
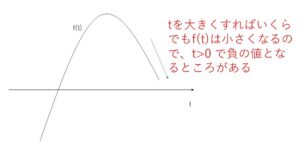
\(f(t)\)は\(t\)の2次関数で上に凸のグラフ。
\(t\)を大きくすれば、\(f(t)\)はいくらでも小さくなるので\(f(t)<0\) となる正の数\(t\)が存在する。
よって \(y>2\)
(ウ)\(2-y>0\)のとき (\(y<2\)のとき)
\(f(t)=\)\((2-y)t^2-4xt+2(x^2+y^2)\)は
\(t\)の2次関数で、下に凸のグラフ。
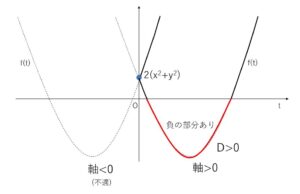
\(y\)切片は、\(2(x^2+y^2)>0\) より、\(f(t)<0\) となる正の数\(t\)が存在するための条件は
\(D>0\) かつ 軸\(>0\)
\(\displaystyle\frac{D}{4}>0\)より
\(4x^2-(2-y)・2(x^2+y^2)\)\(>0\)
\(2x^2-(2x^2+2y^2-x^2y-y^3)\)\(>0\)
\(y(x^2+y^2-2y)\)\(>0\)・・・(i)
ここで \(y<0\) とすると、\(x^2+y^2-2y>0\) となり(i)を満たさない。
よって \(y>0\) かつ \(x^2+y^2-2y>0\)
また、軸は \(t=\displaystyle\frac{2x}{2-y}\) で、\(2-y>0\) だから
\(2x>0\) よって \(x>0\)
まとめると
\(0<y<2\) かつ \(x>0\) かつ \(x^2+(y-1)^2>1\)
以上より範囲を図示すると次の通り。
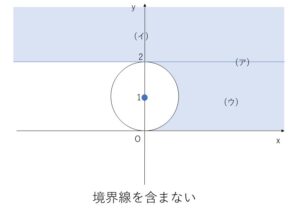
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対称式と領域 back→通過領域①