今回は、領域や最大最小値を求める関数が2次式を含む場合について見ていきます。
やることは1次式のときとさほど変わりません。
(例題1)
\(x,y\)が連立不等式
\(
\begin{eqnarray} \left\{ \begin{array}{l} x^2+ y^2 ≦25 \\ y≧-2x-2 \end{array} \right. \end{eqnarray}
\)
を満たすとき、\(x+y\)の最小値と最大値を求めよ。
(解答)
\(x^2+y^2=25\) と \(y=-2x-2\) の交点を連立して求めると
\(A(-3,4)\) ,\(B(\displaystyle\frac{7}{5},-\displaystyle\frac{24}{5})\)
よって連立不等式を満たす領域を図示すると次の通り。(境界線を含む)
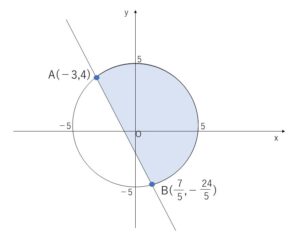
\(x+y=k\)・・・①とおくと、\(y=-x+k\) より①は傾き\(-1\),\(y\)切片が\(k\)の直線です。図示した領域と共有点をもつように\(k\)を変化させて①を動かすと、最小値をとるときは\(k\)(\(y\)切片)が最小となるときなので点\(B\)を①が通るときです。最大値をとるときは\(y\)切片が最大となるときなので、①と円が右上で接するときになります。
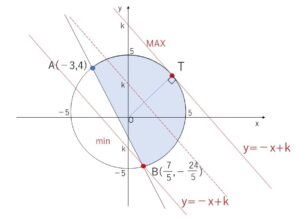
\(x+y=k\)・・・① とおくと、①は傾き\(-1\),\(y\)切片が\(k\)の直線。
①と図示した領域が共有点をもつときを考えると
\(k\)が最小値をとるときは①が\(B(\displaystyle\frac{7}{5},-\displaystyle\frac{24}{5})\)を通るとき。
よって最小値は
\(x+y=\displaystyle\frac{7}{5}-\displaystyle\frac{24}{5}\)\(=\)\(-\displaystyle\frac{17}{5}\) (\(x=\displaystyle\frac{7}{5},y=-\displaystyle\frac{24}{5}\)のとき)
\(k\)が最大値をとるときは①が円\(x^2+y^2=25\)・・・② と第1象限で接するとき。
その接点を\(T\)とすると、\(OT⊥直線①\) より直線\(OT\)の方程式は \(y=x\)・・・③。
②と③を連立すると
\(2x^2=25\)
よって
\(x=±\displaystyle\frac{5\sqrt{2}}{2}\)
\(x>0\) より \(x=\displaystyle\frac{5\sqrt{2}}{2}\) また③より \(y=\displaystyle\frac{5\sqrt{2}}{2}\)
ゆえに最大値は
\(x+y=\displaystyle\frac{5\sqrt{2}}{2}+\displaystyle\frac{5\sqrt{2}}{2}\)\(=\)\(5\sqrt{2}\)
(例題2)
不等式 \(|x-2|≦y≦-|x-2|+4\) が表す領域\(D\)を図示し、点\((x,y)\)がこの領域内を動くとき \(x^2+y^2\) の値の範囲を求めよ。
(解答)
絶対値を外すために、\(x<2\), \(x≧2\) で場合分けします。
\(x<2\) のとき不等式は、\(-(x-2)≦y≦(x-2)+4\) より
\(-x+2≦y≦x+2\)・・・①
\(x≧2\) のとき不等式は、\(x-2≦-(x-2)+4\) より
\(x-2≦y≦-x+6\)・・・②
よって領域\(D\)を図示すると次の通り。
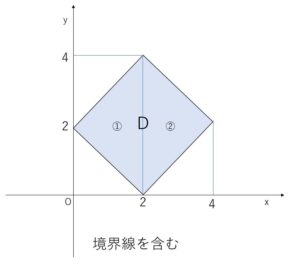
今まで通り \(x^2+y^2=k\)・・・③ とおくと、
\(k=0\) のときは③は原点\((0,0)\)を表し、\(k>0\)のときは中心が原点,半径\(\sqrt{k}\)の円(周)を表します。\(k<0\)は実数の2乗の和なのでありえません。
\(k\)が大きくなるほど円の半径が大きくなるので、\(k\)を\(0\)から徐々に大きくしていき初めて領域\(D\)と共有点をもつときを考えると、円と\(y=-x+2\)が接するときになるので、このときの\(k\)の値が最小値です。
さらに\(k\)を大きくしていくと、\(D\)と共有点をもつぎりぎりのときは、円が点\((2,4)\)と点\((4,2)\)を同時に通るときとなり、このときの\(k\)の値が最大値です。
最小値から最大値の間のときもちゃんと\(D\)と共有点をもつので、答えは
(最小値)\(≦x^2+y^2≦\)(最大値) です。
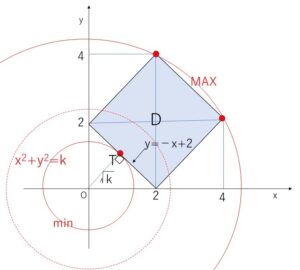
\(x^2+y^2=k\)・・・③ とおくと、\(k=0\) のときは③は原点\((0,0)\)を表し、\(k>0\)のときは中心が原点,半径\(\sqrt{k}\)の円(周)を表す。
\(\sqrt{k}\)が最小値をとるときは\(k\)も最小値をとる。最大値のときも同様である。
③と領域\(D\)が共有点をもつときを考えると
\(k\)が最小値をとるときは、③と直線\(y=-x+2\)・・・④が接するとき。
接点を\(T\)とすると、\(OT\)と④は垂直なので直線\(OT\)の方程式は \(y=x\)・・・⑤
④⑤を連立して交点を求めると、\((1,1)\)
このとき \(k=1^2+1^2=2\)
よって最小値は\(2\)
\(k\)が最大値をとるときは、円③が\((2,4)\),\((4,2)\)を同時に通るときで
\(k=2^2+4^2=4^2+2^2=20\)
よって最大値は\(20\)
\(2<k<20\) のときも円③と\(D\)は共有点をもつのでこれらの値もとりうる。
以上より
\(2≦x^2+y^2≦20\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→領域と最大・最小値①(基礎) next→領域と最大・最小値③(分数式・変換)