指数関数のグラフの性質について見ていきます。
・指数関数のグラフ
\(a>0\), \(a≠1\) のとき
\(y=a^x\)
で表される関数を、\(a\)を底(てい)とする指数関数といいます。
\(y=a^x\) はどのようなグラフになるでしょうか。
例えば、\(a=2,\displaystyle\frac{1}{2}\) の場合について計算しやすい\(x\)の値を何個か代入してみると、次のような表が得られます。
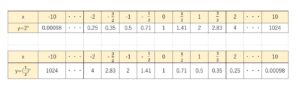
(\(2^{\frac{1}{2}}=\sqrt{2}=1.414\)、\(2^{\frac{3}{2}}=2×2^{\frac{1}{2}}=2\sqrt{2}\) などを用いました)
\(y=2^x\) では、
\(x\)を大きくすると、\(y=2,4,8,16・・・\)と、\(y\)の値も大きくなり、
\(x\)を小さくすると、\(y=\displaystyle\frac{1}{2},\displaystyle\frac{1}{4},\displaystyle\frac{1}{8},\displaystyle\frac{1}{16},・・・,\displaystyle\frac{1}{1024}・・・・\) と\(0\)に近い正の数となっていきます。
反対に \(y=(\displaystyle\frac{1}{2})^x\) では
\(x\)を大きくすると、\(y=\displaystyle\frac{1}{2},\displaystyle\frac{1}{4},\displaystyle\frac{1}{8},\displaystyle\frac{1}{16},・・・,\displaystyle\frac{1}{1024}・・・・\) と\(0\)に近い正の数となっていき、
\(x\)を小さくすると、\(y=2,4,8,16・・・\)と、\(y\)の値が大きくなります。
このことに注意して、値の組 \((x,y)\) を座標平面上にとり、滑らかに結ぶと次のような曲線が得られます。
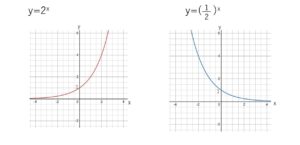
同様に考えると、一般に、
指数関数 \(y=a^x\) のグラフは
①\(a>1\) のときは
\(y=2^x\) のときと同様に、\(x\)が増加すると\(y\)も増加するので(単調増加)、右上がりの曲線
②\(0<a<1\) のとき
\(y=(\displaystyle\frac{1}{2})^x\) のときと同様に、\(x\)が増加すると\(y\)は減少するので(単調減少)、右下がりの曲線
となります。
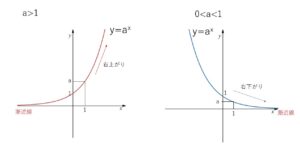
①\(a>1\) のとき、例えば \(y=2^x,3^x,4^x\) などは、「\(x\)→大」 だと2乗,3乗,4乗,5乗・・・と掛け合わされることによって、\(y\)がどんどん大きくなるので右上がりに、
②\(0<a<1\) のとき、例えば \(y=(\displaystyle\frac{1}{2})^x,(\displaystyle\frac{1}{3})^x,(\displaystyle\frac{1}{4})^x\) などは、「\(x\)→大」 だと掛け合わされることによって、\(y\)がどんどん小さくなるので右下がりになります。
また、他に特徴として
(i)グラフより、定義域(\(x\)の範囲)は実数全体で、値域(\(y\)の範囲)は正の数全体
(ii)\(x=0\) を代入すると
\(y=a^0=1\) となるので底\(a\)の値に関わらず、必ず \((0,1)\)を通過し、
(iii)グラフを見ても分かりますが、底\(a\)の値に関わらず\(x\)軸が漸近線となっています。
\(a>1\) のときは \(x\)を極めて小さくすると\(y=0\)(\(x\)軸)に近づき、
\(0<a<1\) のときは \(x\)を極めて大きくすると\(y=0\) (\(x\)軸) に近づくので、\(x\)軸が漸近線になります。
・指数関数のグラフの移動
指数関数のグラフの平行移動,対称移動については、2次関数の場合と同様です。
\(y=a^x\) のグラフを平行or対称移動した後の曲線の方程式は以下の通り
①\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ平行移動
\(y-q=a^{x-p}\)
②\(x\)軸について対称移動
\(-y=a^{x}\)
③\(y\)軸について対称移動
\(y=a^{-x}\)
④原点について対称移動
\(-y=a^{-x}\)
※詳しくは2次関数のところの、→グラフの平行移動、→グラフの対称移動 を参照してください。
最初に考えた、\(y=2^x\) と \(y=(\displaystyle\frac{1}{2})^x\) はちょうど\(y\)軸対称のグラフになっています。
続いて、指数方程式や指数不等式を解いたり、累乗や累乗根の大小関係を決める問題を解くときに必要な知識について見ていきます。
・指数の相等・大小
指数関数のグラフより
\(y=a^x\) について
「\(x\)と\(y\)は1:1対応」 (\(x\)1つにつき\(y\)1つが決定し、さらに反対に\(y\)1つにつき\(x\)1つ決定する) しているので
\(a^p=a^q\) \(⇔\) \(p=q\) (指数の相等)
が成り立ちます。
また同様にグラフより
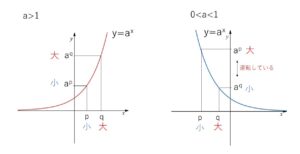
①\(a>1\) のときは、\(x\)が増加すると\(y\)が増加するので、
\(p<q\) \(⇔\) \(a^p<a^q\) (大小一致)
②\(0<a<1\) のときは、\(x\)が増加すると\(y\)が減少するので、
\(p<q\) \(⇔\) \(a^p>a^q\) (大小逆転)
となります。
※②の場合は、指数が大きくなるほど累乗としては小さくなり、逆に累乗が大きくなるほど指数としては小さくなるということです。
一方 \(0<a<1\) では、指数の大小と累乗の大小は逆転することに注意してください。
ここまでは底\(a\)が共通している場合の大小関係について考えましたが、底が共通していない場合の大小関係を次に考えていきます。
・累乗根の相等・大小
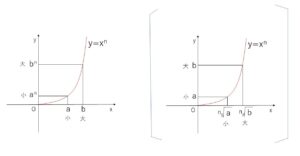
\(n\)を自然数とするとき、\(n\)次関数 \(y=x^n\) (ただし \(x≧0\) の部分) のグラフを考えると、\(n\)の偶奇に関わらず増加関数となるので、指数関数のグラフと同様に\(x,y\)は1:1対応となり、次のことが成り立ちます。
\(a>0\), \(b>0\), \(n\)が自然数のとき
\(a^n=b^n\) \(⇔\) \(a=b\)
また同様にグラフの単調増加性より
\(a>0\), \(b>0\), \(n\)が自然数のとき
\(a<b\) \(⇔\) \(a^n<b^n\)・・・(ア) (大小一致)
(ア)において、\(a\)→\(\sqrt[n]{a}\), \(b\)→\(\sqrt[n]{b}\) とおきかえると
\(\sqrt[n]{a}<\sqrt[n]b\) \(⇔\) \(a<b\)・・・(イ) (大小一致)
(ア)(イ)をまとめると
\(\sqrt[n]{a}<\sqrt[n]b\) \(⇔\) \(a<b\) \(⇔\) \(a^n<b^n\) (大小一致)
が成り立つことになります。
(例題1)
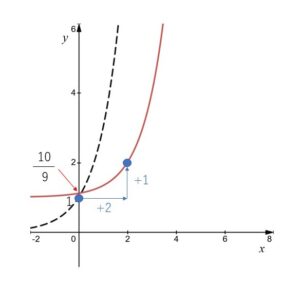
関数 \(y=\displaystyle\frac{1}{3}\cdot3^{x-1}+1\) は
関数 \(y=3^x\) のグラフをどのように移動したものか答えよ。
(解答)
\(y=\displaystyle\frac{1}{3}\cdot3^{x-1}+1\)
\(=3^{-1}\cdot3^{x-1}+1\)
\(=3^{x-2}+1\)
よって
\(y-1=3^{x-2}\) より
\(x\)軸方向に\(2\), \(y\)軸方向に\(1\)だけ平行移動したもの
(例題2)次の3数の大小を比較せよ。
(1)\(\sqrt{2},\sqrt[4]{4},\sqrt[8]{8}\)
(2)\(\sqrt[3]{3},\sqrt[4]{5},\sqrt[5]{6}\)
(解答)
(1)
\(\sqrt{2}=2^{\frac{1}{2}}\)
\(\sqrt[4]{4}=\sqrt[4]{2^2}=2^{\frac{2}{4}}=2^{\frac{1}{2}}\)
\(\sqrt[8]{8}=\sqrt[8]{2^3}=2^{\frac{3}{8}}\)
底は\(2\)で、\(\displaystyle\frac{1}{2}>\displaystyle\frac{3}{8}\) だから
\(\sqrt{2}=\sqrt[4]{4}>\sqrt[8]{8}\)
(別解)
もとの3数を計算できる形にするために、すべてを\(8\)乗(2,4,8の最小公倍数乗)して指数を整数値にします。
\((\sqrt{2})^8=16\)
\((\sqrt[4]{4})^8=(4^{\frac{1}{4}})^8=4^2=16\)
\((\sqrt[8]{8})^8=8\)
\((\sqrt{2})^8=(\sqrt[4]{4})^8>(\sqrt[8]{8})^8\)
と
\(\sqrt{2}>0\), \(\sqrt[4]{4}>0\), \(\sqrt[8]{8}>0\) より
\(\sqrt{2}=\sqrt[4]{4}>\sqrt[8]{8}\)
(2)
ここで3つまとめて比較をしようとすると60乗(3,4,5の最小公倍数乗)することになり計算が大変になるので、2個ずつ分けていきます。
\(\sqrt[3]{3},\sqrt[4]{5},\sqrt[5]{6}\) の大小について考える。
①\(\sqrt[3]{3},\sqrt[4]{5}\) について
\(12\)乗して
\((\sqrt[3]{3})^{12}=3^4=81\)
\((\sqrt[4]{5})^{12}=5^3=125\)
よって、\((\sqrt[3]{3})^{12}<(\sqrt[4]{5})^{12}\) で
\(\sqrt[3]{3}>0,\sqrt[4]{5}>0\) より
\(\sqrt[3]{3}<\sqrt[4]{5}\)
②\(\sqrt[3]{3},\sqrt[5]{6}\) について
\(15\)乗して
\((\sqrt[3]{3})^{15}=3^5=243\)
\((\sqrt[5]{6})^{15}=6^3=216\)
よって、\((\sqrt[3]{3})^{15}>(\sqrt[5]{6})^{15}\) で
\(\sqrt[3]{3}>0,\sqrt[5]{6}>0\) より
\(\sqrt[3]{3}>\sqrt[5]{6}\)
①②から
\(\sqrt[5]{6}<\sqrt[3]{3}<\sqrt[4]{5}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→指数方程式 back→指数の計算②