極値をとる\(x\)のとりうる範囲に関する問題について見ていきます。
(例題1)
3次関数 \(f(x)=x^3+ax^2+bx\) は極大値と極小値をもち、それらを区間 \(-1≦x≦1\) 内でとるものとする。この条件を満たす実数の組 \((a,b)\) の存在範囲を図示せよ。
(解答)
\(f'(x)=3x^2+2ax+b\) より
\(f(x)\)が極値をもち、かつ それらが区間 \(-1≦x≦1\) にある条件は、
2次方程式 \(3x^2+2ax+b=0\) が、この範囲に異なる2つの実数解をもつことである。
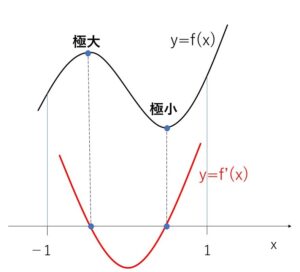
(i) \(\displaystyle\frac{D}{4}>0\)
(ii) \(-1\) ≦ (軸)\(-\displaystyle\frac{1}{3}a\) ≦\(1\)
(iii) \(f'(-1)≧0\), \(f'(1)≧0\)
より
(i) \(a^2-3b>0\)・・・①
(ii) \(-3≦a≦3\)・・・②
(ii) \(3-2a+b≧0\), \(3+2a+b≧0\)・・・③
\((a,b)\) の存在範囲は、①②③を図示すると次の通り
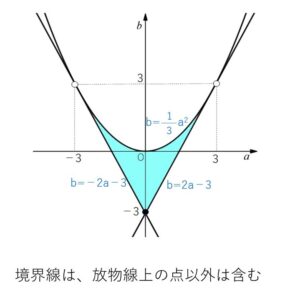
(例題2)
関数 \(y=x^3-3x^2+3ax\) は極値をもつとする。
(1) 極小値を与える\(x\)の値は、どの範囲にあるか。
(2) 極大値、極小値を与える\(x\)がともに \(x>0\) の範囲にあるのは、\(a\)がどのような範囲の値のときか。
(解答)
(1)
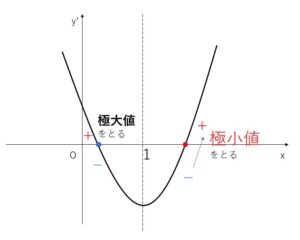
\(y’\)のグラフは、軸が \(x=1\) で固定されていて、あとは\(a\)を変化させると\(y\)軸方向に動く(上下に平行移動する)だけなので、大きい方の解のとりうる範囲は \(x>1\) となりこれが答えになるわけですが、2次方程式の解の公式より大きい方の解が求まるので、解答ではこれを使って範囲を求めてみます。
\(y=x^3-3x^2+3ax\) が極値をもつとき、
\(y’=3(x^2-2x+a)=0\) が異なる2つの実数解をもつときだから
\(\displaystyle\frac{D}{4}=1-a>0\)
よって
\(a<1\)・・・①
また、極小値をとるときの\(x\)は2解のうち大きい方で、解の公式から
\(x=1+\sqrt{1-a}\)
①より
\(x=1+\sqrt{1-a}>1+0=1\)
したがって極小値を与える\(x\)の値の範囲は
\(x>1\)
(2)
(1)より、大きい方の解が \(1\) より大きいことが分かっているので、小さいほうの解が\(0\)より大きい条件を調べても解けます。こちらも解の公式を利用します。
\(y’=3(x^2-2x+a)=0\) の異なる2つの実数解が極値を与える値である。
(1)より2解のうち大きい方は\(1\)より大きいので、小さい方の解が\(0\)より大きい条件を調べればよい。解の公式から
\(x=1-\sqrt{1-a}\)
より
\(1-\sqrt{1-a}>0\)
\(\sqrt{1-a}<1\)・・・②
(1)の① \(a<1\) から②の両辺は正だから2乗して
\(1-a<1\)
\(a>0\)
①と合わせると
\(0<a<1\)
(別解)
\(y’=3(x^2-2x+a)=0\) の異なる2つの実数解がともに \(x>0\) の範囲にあればよいから
\(f'(x)=x^2-2x+a\) とおいて
(i)\(\displaystyle\frac{D}{4}>0\)
(ii) (軸)1 >0
(iii) 端点 \(f'(0)>0\)
(i)\(1-a>0\)
(ii) 常に成り立つ
(iii) \(a>0\)
したがって
\(0<a<1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→最大・最小値の基礎 back→極値をもつ条件