引き続き接線に関する面積の問題について見ていきます。
(例題1)
曲線 \(y=x^3-2x\) について
(1)点\((0,2)\) を通り、この曲線に接する直線\(l\)の方程式を求めよ。
(2)直線\(l\)とこの曲線で囲まれた部分の面積を求めよ。
(解答)
(1)
\(y=x^3-2x\) 上の接点を \((t,t^3-2t)\) とおく。
\(y’=3x^2-2\) より接線の方程式は
\(y=(3t^2-2)(x-t)+t^3-2t\)
整理して
\(y=(3t^2-2)x-2t^3\)・・・①
これが \((0,2)\) を通るから
\(2=-2t^3\)
\(t^3=-1\)
\(t=-1\)
①より接線の方程式は
\(y=x+2\)
(2)
接点以外の交点を求めると
\(x^3-2x=x+2\)
\((x+1)^2(x-2)=0\)
\(x=2\)
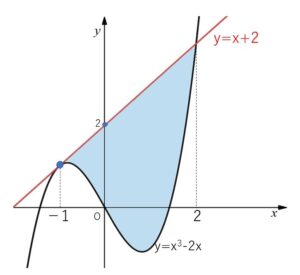
したがって面積\(S\)は
\(S=\displaystyle\int_{-1}^{2}\{x+2-(x^3-2x)\}dx\)
\(=-\displaystyle\int_{-1}^{2}(x+1)^2(x-2)dx\)・・・②
\(=-\displaystyle\int_{-1}^{2}(x+1)^2\{(x+1)-3\}dx\)
\(=-\displaystyle\int_{-1}^{2}(x+1)^3dx+\displaystyle\int_{-1}^{2}3(x+1)^2dx\)
\(=- \left[\displaystyle\frac{(x+1)^4}{4}\right]_{-1}^{2}+\left[(x+1)^3\right]_{-1}^{2}\)
\(=\displaystyle\frac{27}{4}\)
\(S=\displaystyle\frac{1}{12}(2+1)^4=\displaystyle\frac{27}{4}\)
なお、解答の式変形は1/12公式の導出方法と同じです。
(例題2)
関数 \(f(x)=x^4-2x^3-3x^2\), \(g(x)=lx+m\) (ただし、\(l,m\)は実数の定数)
がある。
(1) 曲線 \(y=f(x)\) と 直線 \(y=g(x)\) とが相異なる2点で接するように、\(l,m\)の値を求めよ。
(2) (1)のとき、曲線\(y=f(x)\) と直線\(y=g(x)\) とによって囲まれる部分の面積を求めよ。
(解答)
(1)
2つの接点の\(x\)座標を\(α,β\) (\(α<β\)) とおくと
\(x^4-2x^3-3x^2-(lx+m)=(x-α)^2(x-β)^2\)・・・①
(右辺)
\(=\{(x-α)(x-β)\}^2\)
\(=\{x^2-(α+β)x+αβ\}^2\)
\(=x^4+(α+β)^2x^2+α^2β^2-2(α+β)x^3-2(α+β)αβx+2αβx^2\)
\(=x^4-2(α+β)x^3+\{(α+β)^2+2αβ\}x^2-2αβ(α+β)x+α^2β^2\)
①で係数比較すると
\(-2=-2(α+β)\)・・・②
\(-3=(α+β)^2+2αβ\)・・・③
\(-l=-2αβ(α+β)\)・・・④
\(-m=α^2β^2\)・・・⑤
②③より
\(α+β=1\), \(αβ=-2\)
\(X^2-X-2=0\) の2解を求めると
\((X+1)(X-2)=0\)
\(X=-1,2\)
よって
\(α=-1\), \(β=2\)
④⑤より
\(l=2αβ(α+β)=-4\)
\(m=-(αβ)^2=-4\)
答 \(l=-4\), \(m=-4\)
(2)
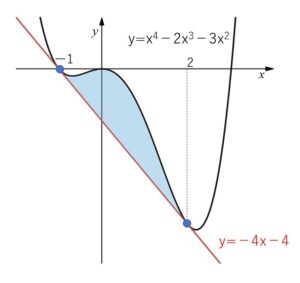
求める面積\(S\)は
\(S=\displaystyle\int_{α}^{β}\{f(x)-g(x)\}dx\)
\(=\displaystyle\int_{-1}^{2}(x+1)^2(x-2)^2dx\)
\(=\displaystyle\int_{-1}^{2}(x+1)^2\{(x+1)-3\}^2dx\)
\(=\displaystyle\int_{-1}^{2}(x+1)^2\{(x+1)^2-6(x+1)+9\}dx\)
\(=\displaystyle\int_{-1}^{2}(x+1)^4dx-\displaystyle\int_{-1}^{2}6(x+1)^3dx+\displaystyle\int_{-1}^{2}9(x+1)^2dx\)
\(=\left[\displaystyle\frac{(x+1)^5}{5}\right]_{-1}^{2}-\left[\displaystyle\frac{3(x+1)^4}{2}\right]_{-1}^{2}+[3(x+1)^3]_{-1}^{2}\)
\(=\displaystyle\frac{243}{5}-\displaystyle\frac{243}{2}+81\)
\(=81(\displaystyle\frac{3}{5}-\displaystyle\frac{3}{2}+1)\)
\(=\displaystyle\frac{81}{10}\)
直接的には接線が登場しませんが、曲線同士が接する例題もやっておきます。
(例題3)
曲線\(C:y=x^3-x\) および 放物線 \(y=x^2+k\) (\(k>0\)) がある。
(1) この放物線と曲線\(C\)が接するとき、\(k\)の値を求めよ。
(2) (1)で定まる放物線と曲線\(C\)で囲まれる部分の面積を求めよ。
(解答)
(1)
\(C:y=x^3-x\) , \(y=x^2+k\) の交点の\(x\)座標を\(t\)とすれば
\(t^3-t=t^2+k\)・・・①
また曲線の方程式をそれぞれ微分して
\(y’=3x^2-1\), \(y=2x\) より
\(3t^2-1=2t\)・・・②
②より
\(3t^2-2t-1=0\)
\((3t+1)(t-1)=0\)
\(t=-\displaystyle\frac{1}{3},1\)
①より
\(k=t^3-t^2-t\) だから
\(t=1\) のとき
\(k=-1\) (\(k>0\)を満たさないので不適)
\(t=-\displaystyle\frac{1}{3}\) のとき
\(k=\displaystyle\frac{5}{27}\) (\(k>0\)を満たす)
(2)
\(h(x)=x^3-x-(x^2+\displaystyle\frac{5}{27})\) とおくと
求める面積\(S\)は、\(y=h(x)\) と\(x\)軸とで囲む面積と等しい。
(接点の\(x\)座標が \(t=-\displaystyle\frac{1}{3}\) であるから、これが重解になることを意識すると)
\(h(x)=x^3-x^2-x-\displaystyle\frac{5}{27}=(x+\displaystyle\frac{1}{3})^2(x-\displaystyle\frac{5}{3})\)
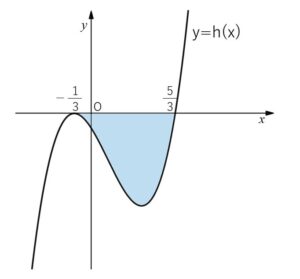
求める面積\(S\)は
\(S=\displaystyle\int_{-\frac{1}{3}}^{\frac{5}{3}}-(x+\displaystyle\frac{1}{3})^2(x-\displaystyle\frac{5}{3})dx\)
\(=-\displaystyle\int_{-\frac{1}{3}}^{\frac{5}{3}}(x+\displaystyle\frac{1}{3})^2\{(x+\displaystyle\frac{1}{3})-2\}dx\)
\(=-\displaystyle\int_{-\frac{1}{3}}^{\frac{5}{3}}(x+\displaystyle\frac{1}{3})^3dx+\displaystyle\int_{-\frac{1}{3}}^{\frac{5}{3}}2(x+\displaystyle\frac{1}{3})^2dx\)
\(=-\left[\displaystyle\frac{1}{4}(x+\displaystyle\frac{1}{3})^4\right]_{-\frac{1}{3}}^{\frac{5}{3}}+\left[\displaystyle\frac{2}{3}(x+\displaystyle\frac{1}{3})^3\right]_{-\frac{1}{3}}^{\frac{5}{3}}\)
\(=-4+\displaystyle\frac{16}{3}\)
\(=\displaystyle\frac{4}{3}\)
また、参考にもとのグラフを図示すると次の通りです。
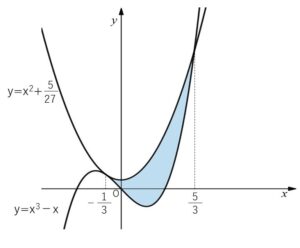
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線と面積③(面積・面積比まとめ) back→接線と面積①