最大最小値が与えられた場合の、2次関数を決定していく問題を見ていきましょう。
(問題1)
\(f(x)=x^2-x+a+1\) (\(a\)は定数)の \(-1≦x≦1\)における最大値が\(6\)となるとき、\(a\)の値はいくつか。
軸も固定、定義域も固定なので簡単です。
(解答)
\(f(x)=(x-\displaystyle\frac{1}{2})^2+a+\displaystyle\frac{3}{4}\)
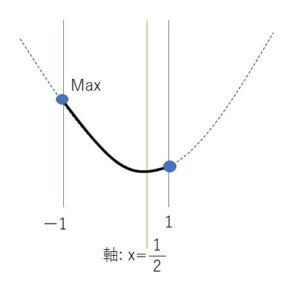
グラフより最大値は \(x=-1\)のときの値なので
\(f(-1)=1+1+a+1=6\)
これを解いて、\(a=3\)
(問題2)
関数 \(y=ax^2-4ax+b\) (\(-1≦x≦3\)) の最大値が\(7\)、最小値が\(-2\)のとき、定数\(a,b\)の値を求めよ。
平方完成すると \(y=a(x-2)^2-4a+b\) なので、軸も定義域も固定です。ただし、aの値によって上に凸・下に凸のグラフの両方が考えられるので、aの正負で場合分けです。問題文の表記が「関数」なので2次関数でない場合(1次関数)も考慮して\(a=0\)も考えます。
(解答)
\(y=f(x)=ax^2-4ax+b=a(x-2)^2-4a+b\) とおく。
\(y=f(x)=ax^2-4ax+b=a(x-2)^2-4a+b\) とおく。
(ア)\(a>0\)のとき
グラフは下に凸となる。軸は \(x=2\) で定義域内にある。
グラフは下に凸となる。軸は \(x=2\) で定義域内にある。
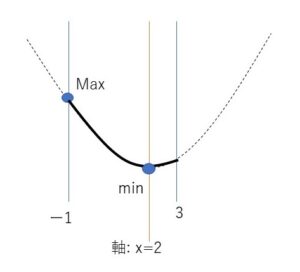
グラフより、
最大値 \(f(-1)=a+4a+b=5a+b=7\)・・・①
最小値 \(f(2)=-4a+b=-2\)・・・②
①②を解いて、\(a=1,b=2\)
これは \(a>0\)を満たす。
最大値 \(f(-1)=a+4a+b=5a+b=7\)・・・①
最小値 \(f(2)=-4a+b=-2\)・・・②
①②を解いて、\(a=1,b=2\)
これは \(a>0\)を満たす。
(イ)\(a=0\)のとき
\(f(x)=b\)となり一定の値をとるから、問題文の条件より不適。
\(f(x)=b\)となり一定の値をとるから、問題文の条件より不適。
(ウ)\(a<0\)のとき
グラフは上に凸のグラフとなる。軸は\(x=2\)で定義域内にある。
グラフは上に凸のグラフとなる。軸は\(x=2\)で定義域内にある。
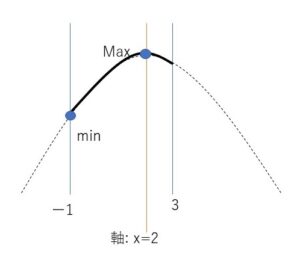
グラフより
最大値 \(f(2)=-4a+b=7\)・・・③
最小値 \(f(-1)=5a+b=-2\)・・・④
③④を解いて,\(a=-1,b=3\)
これは\(a<0\)を満たす。
最大値 \(f(2)=-4a+b=7\)・・・③
最小値 \(f(-1)=5a+b=-2\)・・・④
③④を解いて,\(a=-1,b=3\)
これは\(a<0\)を満たす。
以上(ア)~(ウ)より
\(a=1,b=2\) または \(a=-1,b=3\)
\(a=1,b=2\) または \(a=-1,b=3\)
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。
ここまで読んで下さりありがとうございました。