ベクトルに関する三角形の面積公式について見ていきます。
①ベクトル表記のもの ②成分表示のもの
がありますが、どちらも重要公式です。なお①については空間ベクトルにおいても同じ式になります。
・ベクトルと三角形の面積
\(\sinθ\) については内積の関係式から\(\cosθ\) 経由で求めます。
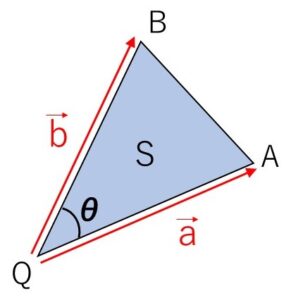
\(△QAB\) において、\(\overrightarrow{QA}=\vec{a}\), \(\overrightarrow{QB}=\vec{b}\), \(\angle AQB=θ\) (\(0°<θ<180°\)) とする。
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\) と \(\sinθ>0\) より
\(\sin \theta=\sqrt{1-\left(\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\right)^2}=\displaystyle\frac{\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}{|\vec{a}||\vec{b}|}\)
\(S=\displaystyle\frac{1}{2}|\vec{a}||\vec{b}|\sinθ\) より
\(S=\displaystyle\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}\)・・・① (ベクトル表記の面積公式)
また座標平面上で考えると、特に\(Q\)が原点\(O\)のとき
\(A(a_1,a_2)\), \(B(b_1,b_2)\) とすると、\(\vec{a}=(a_1,a_2)\), \(\vec{b}=(b_1,b_2)\) になるので、
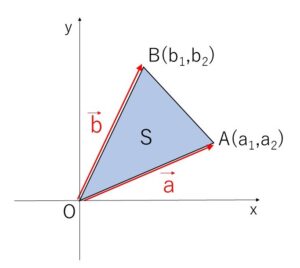
①のルートの中身は
\(|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2\)
\(=(a_1^2+a_2^2)(b_1^2+b_2^2)-(a_1b_1+a_2b_2)^2\)
\(=a_1^2b_2^2-2a_1b_1a_2b_2+a_2^2b_1^2\)
\(=(a_1b_2-a_2b_1)^2\)
となるので
\(S=\displaystyle\frac{1}{2}\sqrt{(a_1b_2-a_2b_1)^2}\) より
\(S=\displaystyle\frac{1}{2}|a_1b_2-a_2b_1|\) (成分表示の面積公式)
(例題1)
(1)\(|\overrightarrow{OA}|=5\), \(|\overrightarrow{OB}|=3\), \(\overrightarrow{OA}\cdot\overrightarrow{OB}=7\) のとき、\(△OAB\) の面積を求めよ。
(2)\(A(1,3)\), \(B(4,-1)\), \(C(5,5)\) のとき、\(△ABC\) の面積を求めよ。
(解答)
(1)
\(S=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{OA}|^2|\overrightarrow{OB}|^2-(\overrightarrow{OA}\cdot\overrightarrow{OB})^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{25\cdot9-49}\)
\(=2\sqrt{11}\)
(2)
\(A(1,3)\), \(B(4,-1)\), \(C(5,5)\) を \(A\)が原点にくるように平行移動すると
\(A'(1-1,3-3)\), \(B'(4-1,-1-3)\), \(C'(5-1,5-3)\)
つまり移動後の3点は
\(A'(0,0)\), \(B'(3,-4)\), \(C'(4,2)\)
\(S=\displaystyle\frac{1}{2}|3\cdot2-(-4)\cdot4|\)\(=11\)
(例題2)
4点 \(A(-2,1)\), \(B(\fbox{ア},4)\), \(C(4,\fbox{イ})\), \(D(-1,3)\) を頂点とする四角形\(ABCD\)は、面積が \(\fbox{ウ}\) の平行四辺形である。
(解答)
\(B(x,4)\), \(C(4,y)\) とおくと
\(\overrightarrow{AB}=\overrightarrow{DC}\) より
\((x+2,3)=(5,y-3)\)
\(x+2=5\), \(3=y-3\) より
\(x=3\)・・・(ア) \(y=6\)・・・(イ)
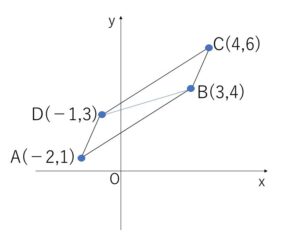
\(△ABD\)について、\(A\)が原点にくるように平行移動すると3点\(A,B,D\)は
\(A'(0,0)\), \(D'(1,2)\), \(B'(5,3)\) となるから
平行四辺形の面積\(S\)は
\(S=2△ABD\)
\(=2×\displaystyle\frac{1}{2}|1\cdot3-2\cdot5|\)
\(=7\)・・・(ウ)
(例題3)
平面上の3点\(O,A,B\)は、条件
\(|\overrightarrow{OA}|=|\overrightarrow{OA}+\overrightarrow{OB}|=|2\overrightarrow{OA}+\overrightarrow{OB}|=1\)
を満たす。このとき\(△OAB\)の面積を求めよ。
ベクトルの表記の公式を使うなら \(\overrightarrow{OA}\cdot\overrightarrow{OB}\)、
\(S=\displaystyle\frac{1}{2}ab\sinθ\) を使うなら \(\sinθ\) (\(\cosθ\)経由で求める)が必要です。解答では前者の方法で行きたいと思います。
(解答)
\(|\overrightarrow{OA}|^2=|\overrightarrow{OA}+\overrightarrow{OB}|^2\) より
\(|\overrightarrow{OA}|^2=|\overrightarrow{OA}|^2+2\overrightarrow{OA}\cdot\overrightarrow{OB}+|\overrightarrow{OB}|^2\)
よって
\(2\overrightarrow{OA}\cdot\overrightarrow{OB}+|\overrightarrow{OB}|^2=0\)・・・①
\(|\overrightarrow{OA}+\overrightarrow{OB}|^2=|2\overrightarrow{OA}+\overrightarrow{OB}|^2\) より
\(|\overrightarrow{OA}|^2+2\overrightarrow{OA}\cdot\overrightarrow{OB}+|\overrightarrow{OB}|^2=4|\overrightarrow{OA}|^2+4\overrightarrow{OA}\cdot\overrightarrow{OB}+|\overrightarrow{OB}|^2\)
\(|\overrightarrow{OA}|=1\) より整理すると
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=-\displaystyle\frac{3}{2}\)・・・②
②を①に代入して
\(-3+|\overrightarrow{OB}|^2=0\)
\(|\overrightarrow{OB}|=\sqrt{3}\)
したがって\(△OAB\)の面積\(S\)は
\(S=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{OA}|^2|\overrightarrow{OB}|^2-(\overrightarrow{OA}\cdot\overrightarrow{OB})^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{1\cdot3-(\displaystyle\frac{3}{2})^2}\)
\(=\displaystyle\frac{\sqrt{3}}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→正五角形とベクトル back→内積と等式・不等式の証明