\(x\)の2次関数の最大最小値を求めたとき、それが\(x\)ではない文字を含む場合は、最大最小値をさらにその文字についての関数とみることができます。
(問題)
(\(0≦x≦1\))のとき、\(f(x)=x^2-2ax+\displaystyle\frac{a}{4}\)の最小値を\(m\)とする。
(1)\(m\)を\(a\)の式で表せ。
(2)\(m\)を最大にする\(a\)の値、および\(m\)の最大値を求めよ。
(1)は定義域固定の、軸が動くパターンです。→(4-4)軸が動く最大最小 軸と定義域の位置関係で場合分けです。
(解答)
(1)
\(f(x)=(x-a)^2-a^2+\displaystyle\frac{a}{4}\)
(1)
\(f(x)=(x-a)^2-a^2+\displaystyle\frac{a}{4}\)
定義域の左側に軸がある場合、\(a<0\)・・・①
定義域の中に軸がある場合、\(0≦a≦1\)・・・②
定義域の右側に軸がある場合、\(a>1\)・・・③
定義域の中に軸がある場合、\(0≦a≦1\)・・・②
定義域の右側に軸がある場合、\(a>1\)・・・③
①\(a<0\)のとき
\(m=f(0)=\displaystyle\frac{a}{4}\)
\(m=f(0)=\displaystyle\frac{a}{4}\)
②\(0≦a≦1\)のとき
\(m=f(a)=-a^2+\displaystyle\frac{a}{4}\)
\(m=f(a)=-a^2+\displaystyle\frac{a}{4}\)
③\(a>1\)のとき
\(m=f(1)=1-\displaystyle\frac{7a}{4}\)
\(m=f(1)=1-\displaystyle\frac{7a}{4}\)
(2)
(1)の結果から、\(m\)は\(a\)の新たな関数とみることができます(定義域によって式が異なる関数です)。グラフを書いて最大値を求めましょう。\(a\)の関数なのでグラフの横軸は\(a\)となります。
(1)の②は
\(m=-a^2+\displaystyle\frac{a}{4}=-(a-\displaystyle\frac{1}{8})^2+\displaystyle\frac{1}{64}\)で
(1)の結果をグラフにすると以下のようになる。
\(m=-a^2+\displaystyle\frac{a}{4}=-(a-\displaystyle\frac{1}{8})^2+\displaystyle\frac{1}{64}\)で
(1)の結果をグラフにすると以下のようになる。
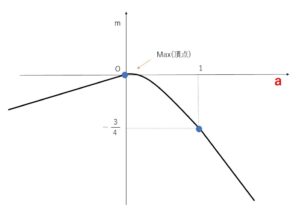
グラフより最大値は \(a=\displaystyle\frac{1}{8}\)のとき \(\displaystyle\frac{1}{64}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。