球面の方程式の基礎的な演習です。
(例題1)
(1)\(A(5,-5,-2)\), \(B(-3,-1,6)\) を直径の両端とする球面の方程式を求めよ。
(2)点\((1,1,2)\) を通り、3つの座標平面に接する球面の方程式を求めよ。
(3)中心を\((1,-5,2)\)とし、\(y\)軸と接する球面の方程式を求めよ。
(解答)
(1)
中心の座標は
\((\displaystyle\frac{5-3}{2},\displaystyle\frac{-5-1}{2},\displaystyle\frac{-2+6}{2})=(1,-3,2)\)
半径は中心と\(A(5,-5,-2)\)の距離だから
\(\sqrt{4^2+(-2)^2+(-4)^2}=6\)
したがって球面の方程式は
\((x-1)^2+(y+3)^2+(z-2)^2=36\)
(別解)
球面上の点を \(P(x,y,z)\) とおくと
\(\overrightarrow{AP}\cdot\overrightarrow{BP}=0\)
\(A(5,-5,-2)\), \(B(-3,-1,6)\) より
\((x-5,y+5,z+2)\cdot(x+3,y+1,z-6)=0\)
\((x-5)(x+3)+(y+5)(y+1)+(z+2)(z-6)=0\)
よって
\(x^2-2x+y^2+6y+z^2-4y-22=0\)
(2)
3つの座標平面に接していて、点\((1,1,2)\)を通るので中心の\(x,y,z\)座標はすべて正です。そして\(xy\)平面に接しているので、\((xy平面からの距離)=(半径)\) となるために、球面の中心の\(z\)座標が半径\(r\)と同じになります。\(yz,zx\)平面も同様なので、中心の座標は \((r,r,r)\) です。
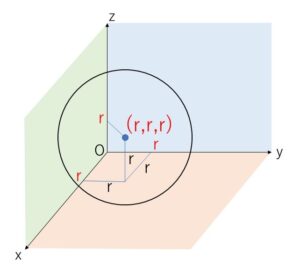
半径を\(r(>0)\)とすると、中心は \((r,r,r)\) となるから球面の方程式は
\((x-r)^2+(y-r)^2+(z-r)^2=r^2\)
点\((1,1,2)\) を通るから
\((1-r)^2+(1-r)^2+(2-r)^2=r^2\)
\(r^2-4r+3=0\)
\((r-1)(r-3)=0\)
\(r=1,3\) (\(r>0\)を満たす)
よって球面の方程式は
\((x-1)^2+(y-1)^2+(z-1)^2=1\)
または
\((x-3)^2+(y-3)^2+(z-3)^2=9\)
(3)
接点の座標(\(y\)軸上にある)がポイントとなりますが、球面の中心と\(y\)軸を通る平面で考えると、中心から\(y\)軸に下ろした垂線の足が接点となることが分かります。
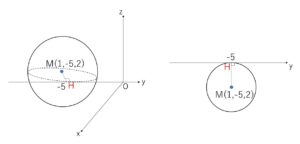
接点を\(H\)とすると、その座標は \(H(0,-5,0)\)
よって半径は、中心\((1,-5,2)\)と\(H\)の距離だから
\(\sqrt{1^2+0^2+2^2}=\sqrt{5}\)
したがって求める球面の方程式は
\((x-1)^2+(y+5)^2+(z-2)^2=5\)
(例題2)
4点 \((0,0,0)\), \((1,-2,0)\), \((3,-2,2)\), \((3,0,0)\) を通る球面の方程式を求めよ。
一般形 \(x^2+y^2+z^2+Ax+By+Cz+D=0\)
に代入して、\(A,B,C,D\)を求めていきます。
(解答)
球面の方程式を
\(x^2+y^2+z^2+Ax+By+Cz+D=0\) とおく。
\((0,0,0)\), \((1,-2,0)\), \((3,-2,2)\), \((3,0,0)\) を通るから
\(D=0\)・・・①
\(1+4+A-2B+D=0\)・・・②
\(9+4+4+3A-2B+2C+D=0\)・・・③
\(9+3A+D=0\)・・・④
①④より \(A=-3\)
②より \(5-3-2B=0\)
よって \(B=1\)
③より
\(17-9-2+2C=0\)
\(C=-3\)
したがって
\(x^2+y^2+z^2-3x+y-3z=0\)
(例題3)
空間内に3点 \(A(1,0,0)\), \(B(0,2,0)\), \(C(0,0,3)\) をとる。
(1)空間内の点\(P\)が \(\overrightarrow{AP}\cdot(\overrightarrow{BP}+2\overrightarrow{CP})=0\) をみたしながら動くとき、この点\(P\)はある定点\(Q\)から一定の距離にあることを示し、点\(Q\)の座標およびその距離を求めよ。
(2) (1)における定点\(Q\)は3点\(A,B,C\)を通る平面上にあることを示せ。
(3) (1)における\(P\)について、四面体\(ABCP\)の体積の最大値を求めよ。
(解答)
(1)
(始点を\(A\)に合わせると)
\(\overrightarrow{AP}\cdot(\overrightarrow{BP}+2\overrightarrow{CP})=0\) より
\(\overrightarrow{AP}\cdot(3\overrightarrow{AP}-\overrightarrow{AB}-2\overrightarrow{AC})=0\)
\(3(|\overrightarrow{AP}|^2-\displaystyle\frac{(\overrightarrow{AB}+2\overrightarrow{AC})\cdot\overrightarrow{AP}}{3})=0\)
(平方完成すると)
\(3\left|\overrightarrow{AP}-\displaystyle\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{6}\right|^2-\displaystyle\frac{|\overrightarrow{AB}+2\overrightarrow{AC}|^2}{12}=0\)
よって
\(\left|\overrightarrow{AP}-\displaystyle\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{6}\right|^2=\displaystyle\frac{|\overrightarrow{AB}+2\overrightarrow{AC}|^2}{36}\)・・・①
ここで、\(A(1,0,0)\), \(B(0,2,0)\), \(C(0,0,3)\) より
\(\overrightarrow{AB}=(-1,2,0)\), \(\overrightarrow{AC}=(-1,0,3)\) となるから
①の右辺は
\(\displaystyle\frac{|\overrightarrow{AB}+2\overrightarrow{AC}|^2}{36}\)\(=\displaystyle\frac{|(-3,2,6)|^2}{36}\)\(=\displaystyle\frac{49}{36}\)
また①の左辺について
\(\overrightarrow{AQ}=\displaystyle\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{6}\)(\(=\displaystyle\frac{1}{6}(-3,2,6)\))・・・② とおくと、①は
\(|\overrightarrow{AP}-\overrightarrow{AQ}|^2=\displaystyle\frac{49}{36}\)
ゆえに
\(|\overrightarrow{QP}|=\displaystyle\frac{7}{6}\)・・・③
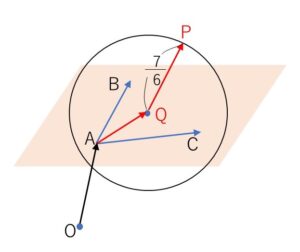
①より
\(\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{AQ}\)
\(=(1,0,0)+\displaystyle\frac{1}{6}(-3,2,6)\)
\(=(\displaystyle\frac{1}{2},\displaystyle\frac{1}{3},1)\)
したがって\(Q\)は定点で、③より点\(P\)は定点\(Q\)から一定の距離\(\displaystyle\frac{7}{6}\) にある。
答 \(Q(\displaystyle\frac{1}{2},\displaystyle\frac{1}{3},1)\), 距離 \(\displaystyle\frac{7}{6}\)
(2)
(1)の②より
\(\overrightarrow{AQ}=\displaystyle\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{6}\)
よって\(Q\)は\(A,B,C\)を通る平面上にある。
(3)
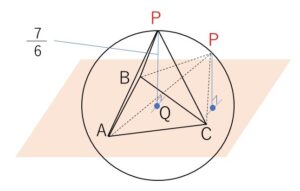
(1)より\(P\)は\(Q\)を中心とし、半径\(\displaystyle\frac{7}{6}\)の球面上にある。
\(△ABC\)を底面とすると、四面体\(ABCP\)の体積が最大となるときは高さが最大となるときで、高さの最大値は\(\displaystyle\frac{7}{6}\)となる。
\(△ABC=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot\overrightarrow{AC})^2}\)
\(\overrightarrow{AB}=(-1,2,0)\), \(\overrightarrow{AC}=(-1,0,3)\) より
\(△ABC=\displaystyle\frac{1}{2}\sqrt{5\cdot10-1^2}\)\(=\displaystyle\frac{7}{2}\)
よって体積の最大値\(V\)は
\(V=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{7}{2}\cdot\displaystyle\frac{7}{6}\)\(=\displaystyle\frac{49}{36}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→球面と直線・交点の個数 back→球面の方程式①