三角関数の極限について見ていきます。
・三角関数の極限
\(y=\sin x\)、\(y=\cos x\)、\(y=\tan x\) のグラフは次の通りです。
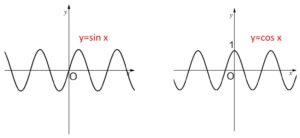
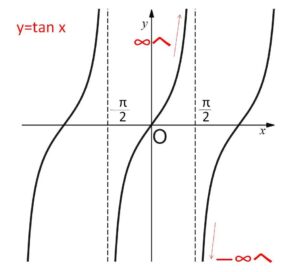
これらのグラフから、まずは\(\sin x,\cos x\)については、\(1\)と\(-1\)の間を行ったりきたりするので
\(\displaystyle\lim_{x \to \infty}\sin x,\ \displaystyle\lim_{x \to -\infty}\sin x\)、\(\displaystyle\lim_{x \to \infty}\cos x,\ \displaystyle\lim_{x \to -\infty}\cos x\) のいずれについても極限は存在しません。
また、\(\tan x\) については漸近線が \(x=\displaystyle\frac{π}{2}+kπ\) (\(k\)は整数) なのでこの前後の極限を考えると、例えば \(x=\displaystyle\frac{π}{2}\) だと右側極限・左側極限はそれぞれ
\(\displaystyle\lim_{x \to \frac{π}{2}+0}\tan x=-\infty\)、\(\displaystyle\lim_{x \to \frac{π}{2}-0}\tan x=\infty\)
になります。(\(\displaystyle\lim_{x \to \frac{π}{2}}\tan x\)は存在しないことになる)
・極限 \(\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}\)
角を弧度法で表すとき、\(\displaystyle\frac{\sin x}{x}\) について次の極限に関する式が成り立ちます。
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}=1\) (\(\displaystyle\lim_{x \to 0}\displaystyle\frac{x}{\sin x}=1\))
また、これらを用いると\(\tan x\)についても同様の式が成り立つことが分かる。
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{\tan x}{x}=1\) (\(\displaystyle\lim_{x \to 0}\displaystyle\frac{x}{\tan x}=1\))
(解説)
\(x \to 0\) なので、\(x\)は\(0\)に近い絶対値が小さな値として扱ってよい。よって \(0<|x|<\displaystyle\frac{π}{2}\) として(このくらいの範囲設定で十分)、扇形の面積と三角形の面積の大小関係からはさみうちで求める。
(1)まずは右側極限 \(\displaystyle\lim_{x \to +0}\displaystyle\frac{\sin x}{x}\) について
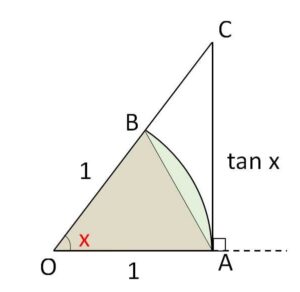
\(0<x<\displaystyle\frac{π}{2}\) (正の値) のとき、図のように「半径\(1\)、中心角\(x\)の扇形\(OAB\)」と三角形を考える。(ただし直線\(AC\)と扇形は\(A\)で接している)
\(△OAB\)<扇形\(OAB\)<\(△OAC\)
より
\(\displaystyle\frac{1}{2}\cdot1^2\cdot\sin x<\displaystyle\frac{1}{2}\cdot1^2\cdot x<\displaystyle\frac{1}{2}\cdot1\cdot\tan x\)
よって
\(\sin x<x<\tan x\)
が成り立つ。辺々\(\sin x\ (>0)\) で割って逆数をとると(不等号の向きが変わって)
\(\cos x<\displaystyle\frac{\sin x}{x}<1\)
\(\displaystyle\lim_{x \to +0}\cos x=1\) だからはさみうちの原理より
\(\displaystyle\lim_{x \to +0}\displaystyle\frac{\sin x}{x}=1\)・・・①
(2)左側極限について
\(-\displaystyle\frac{π}{2}<x<0\) のとき、\(x=-t\) と変換すると
\(x \to -0\) のとき、\(t \to +0\) となるから
\(\displaystyle\lim_{x \to -0}\displaystyle\frac{\sin x}{x}\)
\(=\displaystyle\lim_{t \to +0}\displaystyle\frac{\sin(-t)}{-t}=\displaystyle\lim_{t \to +0}\displaystyle\frac{-\sin t}{-t}=\displaystyle\lim_{t \to +0}\displaystyle\frac{\sin t}{t}\)
\(=1\) (①より)
したがって右側極限と左側極限が一致して
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}=1\)
また
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{x}{\sin x}=\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{\displaystyle\frac{\sin x}{x}}=1\)
さらに\(\tan x\) についても
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{\tan x}{x}\)\(=\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}\cdot\displaystyle\frac{1}{\cos x}\)\(=1\)
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{x}{\tan x}=\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{\displaystyle\frac{\tan x}{x}}=1\)
(注)
角は弧度法を用いることに気をつけください。度数法を用いると扇形の面積が
\(1^2\cdot π\cdot\displaystyle\frac{x}{360}=\displaystyle\frac{π}{360}x\)
となるので、同様の議論により
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{\sin x}{x}=\displaystyle\frac{π}{180}\)
となります。
弧度法を用いたほうが極限の式がスッキリするので、極限やそれを利用する微分・積分では基本的には弧度法を用います。
試験などで証明が問われた場合には上の証明方法で問題ないと思いますが、この証明では扇形の面積公式 \(S=\displaystyle\frac{1}{2}r^2θ\) が成り立つことを前提にしています。ここで扇形の面積\(S\)を仮に積分を用いて求めることにすると、全体の円の面積 \(S_0=2\displaystyle\int_{-1}^{1}\sqrt{1-x^2}dx\) (またはこの積分範囲の1部分の積分)を計算することになります。積分計算に \(x=\sinθ\) による置換積分を用いると、\(\sinθ\)の微分が必要になりますが、この微分の導出には \(\displaystyle\lim_{θ \to 0}\displaystyle\frac{\sinθ}{θ}=1\) が必要です。すると \(\displaystyle\lim_{θ \to 0}\displaystyle\frac{\sinθ}{θ}=1\) の証明に \(\displaystyle\lim_{θ \to 0}\displaystyle\frac{\sinθ}{θ}=1\) を用いてしまっていることになり、循環論法になってしまいます。
これを避けるためには別の論理構成(積分の計算を別の方法にするなど)を選ぶことになりますが、興味のある方は調べてみてください。
演習は次回以降にします。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の極限② back→指数・対数関数の極限(関数)