曲線と曲線の距離に関する例題です。
(例題)
平面上に2つの曲線
\(C:y=e^{2x}+1\)
\(D:y=-x^2+14x-49\)
がある。点\(P,Q\) がそれぞれ\(C\)上と\(D\)上を動くとき、線分\(PQ\)の長さの最小値を求めよ。
それと一応、2曲線が交わらないことの確認はしておきます。(交わるときには線分の長さの最小値は\(0\)になるが、\(P,Q\)が一致して※で考えられない)
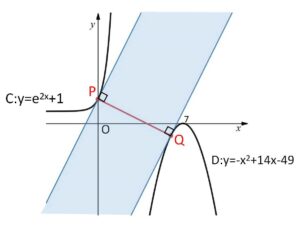
曲線\(C\)は下に凸、曲線\(D\)は上に凸のグラフ。
また \(C:y=e^{2x}+1>0\)、\(D:y=-(x-7)^2≦0\) より、\(C,D\)は交わらない。
よって、点\(P,Q\)における接線の傾きが等しく、直線\(PQ\)がこれらの接線に垂直になるときがあれば、線分\(PQ\)の長さは最小となる。
\(f(x)=e^{2x}+1\)
\(g(x)=-x^2+14x-49\)
とおくと
\(f'(x)=2e^{2x}\)
\(g'(x)=-2x+14\)
\(P(p,f(p))\)、\(Q(q,g(q))\) とおくと、接線の傾きが等しいから
\(2e^{2p}=-2q+14\)
ゆえに
\(q=-e^{2p}+7\)・・・①
また、\(PQ\)と接線が垂直なので
\(\displaystyle\frac{f(p)-f(q)}{p-q}\cdot 2e^{2p}=-1\)・・・②
(図より、\(p=q\) とはならない)
②より
\(\{e^{2p}+1+(q-7)^2\}\cdot2e^{2p}=-(p-q)\)
①\(q=-e^{2p}+7\) を代入して
\(\{e^{2p}+1+e^{4p}\}\cdot2e^{2p}\)\(=-(p+e^{2p}-7)\)
整理すると
\(2e^{6p}+2e^{4p}+3e^{2p}+p-7=0\)・・・③
しかし色々\(p\)に代入することで、\(p=0\) が解であることは分かります。
最初の図から他に解はないことは分かりますが、一応他に解があるかどうかを確認しておきます。(左辺のグラフの単調増加性により解は1つしかない)
③は \(p=0\) を解にもつが、
\(h(p)=2e^{6p}+2e^{4p}+3e^{2p}+p-7\) とおくと
\(h'(p)=12e^{6p}+8e^{4p}+6e^{2p}+1>0\) より
\(h(p)\) は単調増加関数だから、他に解は存在しない。
①より、\(q=6\) となるから\(P,Q\)の座標は
\(P(0,2)\)、\(Q(6,-1)\)
したがって線分\(PQ\)の長さの最小値は
\(\sqrt{6^2+(-3)^2}\)
\(=3\sqrt{5}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→速度・加速度(直線上の運動) back→凸関数(演習)