面積の最大最小問題です。
定積分で面積を求めて微分するのが基本となります。
(例題1)
\(t≧0\) とし、\(y=xe^{-x}\)、\(x=t\)、\(x=2t\) および \(x\)軸の囲む図形の面積を\(S(t)\)とする。
(1)\(S(t)\)を求めよ。
(2)\(S(t)\)の最大値を求めよ。
(解答)
(1)
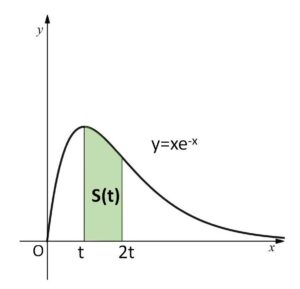
\(x≧0\) のとき \(y=xe^{-x}≧0\) だから
\(S(t)=\displaystyle\int_{t}^{2t}xe^{-x}dx\)
(部分積分をして)
\(=[x(-e^{-x})]_{t}^{2t}+\displaystyle\int_{t}^{2t}e^{-x}dx\)
\(=-2te^{-2t}+te^{-t}+[-e^{-x}]_{t}^{2t}\)
\(=-(2t+1)e^{-2t}+(t+1)e^{-t}\)
(2)
\(S(t)=-(2t+1)e^{-2t}+(t+1)e^{-t}\) (\(t≧0\)) より
\(S'(t)=-2e^{-2t}+(2t+1)\cdot2e^{-2t}+e^{-t}-(t+1)e^{-t}\)
\(=4te^{-2t}-te^{-t}\)
\(=te^{-2t}(4-e^{t})\)
\(t>0\) のとき \(te^{-2t}>0\) だから
\(S(t)\) は \(4-e^{t}=0\) を満たす\(t\)の値で最大値をとる。
よって \(t=\log 4\) のとき
最大値
\(S(\log 4)=-(2\log 4+1)e^{-2\log4}+(\log 4+1)e^{-\log4}\)
\(=-(2\log 4+1)e^{\log\frac{1}{16}}+(\log 4+1)e^{\log\frac{1}{4}}\)
\(=-\displaystyle\frac{1}{16}(2\log 4+1)+\displaystyle\frac{1}{4}(\log 4+1)\)
\(=\displaystyle\frac{1}{8}\log 4+\displaystyle\frac{3}{16}\)
\(=\displaystyle\frac{1}{4}\log 2+\displaystyle\frac{3}{16}\)
(例題2)
実数\(a,b\)に対して、直線 \(l:y=ax+b\) は 曲線 \(C:y=\log(x+1)\) と\(x\)座標が \(0≦x≦e-1\) を満たす点で接しているとする。
(1)\(a,b\)の関係式を求めよ。
(2)曲線\(C\)および3つの直線 \(l\)、\(x=0\)、\(x=e-1\) で囲まれた図形の面積を最小にする\(a,b\)の値と、このときの面積を求めよ。
(解答)
(1)
\(y=\log(x+1)\) を微分すると
\(y’=\displaystyle\frac{1}{x+1}\)
接点の\(x\)座標を\(t\)とおくと
\(0≦t≦e-1\)・・・①
接線の方程式は
\(y=\displaystyle\frac{1}{t+1}(x-t)+\log(t+1)\)
整理して
\(y=\displaystyle\frac{1}{t+1}x-\displaystyle\frac{t}{t+1}+\log(t+1)\)
これと \(y=ax+b\) を比べると
\(a=\displaystyle\frac{1}{t+1}\)・・・②
\(b=-\displaystyle\frac{t}{t+1}+\log(t+1)\)・・・③
(\(t\)を消去して\(a,b\)の関係式を導きます)
②より
\(t=\displaystyle\frac{1}{a}-1\)・・・④
④を①と③に代入して
\(0≦\displaystyle\frac{1}{a}-1≦e-1\)
\(b=-\displaystyle\frac{\displaystyle\frac{1}{a}-1}{\displaystyle\frac{1}{a}}+\log(\displaystyle\frac{1}{a})\)
したがって
\(1≦\displaystyle\frac{1}{a}≦e\)
\(b=a-1-\log a\)
となるから
\(\displaystyle\frac{1}{e}≦a≦1\)
\(b=a-1-\log a\)
(2)
関数の差をとって積分する際に、固定された関数 \(y=\log(x+1)\) の方は一定になるので、微分する際には実質的には接線のほうの積分(台形、三角形の面積)だけを検討していることになります。
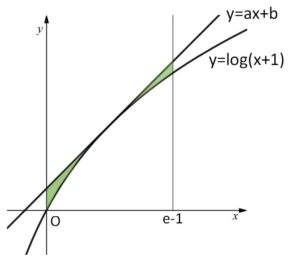
\(y=\log(x+1)\)は上に凸の曲線なので、接線の方が上側にある。
面積を\(S\)とすると
\(S=\displaystyle\int_{0}^{e-1}\{ax+b-\log(x+1)\}dx\)
(\(\log\)の積分は部分積分をして)
\(=\left[\displaystyle\frac{a}{2}x^2+bx-(x+1)\log(x+1)+x\right]_{0}^{e-1}\)
\(=\displaystyle\frac{a}{2}(e-1)^2+b(e-1)-e\log e+(e-1)\)
\(=\displaystyle\frac{a}{2}(e-1)^2+b(e-1)-1\)
(1)より
\(b=a-1-\log a\)
であり、\(b\)を消去すると面積\(S\)は\(a\)の関数となるので改めて\(S(a)\)とおくと
\(S(a)=\displaystyle\frac{a}{2}(e-1)^2+(a-1-\log a)(e-1)-1\)
\(=\displaystyle\frac{e^2-1}{2}a-(e-1)\log a-e\) (\(\displaystyle\frac{1}{e}≦a≦1\))
微分して
\(S'(a)=\displaystyle\frac{e^2-1}{2}-\displaystyle\frac{e-1}{a}\)
\(=\displaystyle\frac{(e^2-1)(a-\displaystyle\frac{2}{e+1})}{2a}\)
\(a=\displaystyle\frac{2}{e+1}\) は \(\displaystyle\frac{1}{e}≦a≦1\) の範囲にあるので
最小値は \(a=\displaystyle\frac{2}{e+1}\) のときにとる。
このとき
\(b=\displaystyle\frac{2}{e+1}-1-\log \displaystyle\frac{2}{e+1}\)
\(=\displaystyle\frac{-e+1}{e+1}+\log\displaystyle\frac{e+1}{2}\)
面積は
\(S(\displaystyle\frac{2}{e+1})=\displaystyle\frac{e^2-1}{2}\cdot\displaystyle\frac{2}{e+1}-(e-1)\log \displaystyle\frac{2}{e+1}-e\)
\(=e-1+(e-1)\log\displaystyle\frac{e+1}{2}-e\)
\(=(e-1)\log\displaystyle\frac{e+1}{2}-1\)
以上になります。お疲れさまでした。
next→陰関数と面積 back→接線と面積