立体の共通部分の体積を求める例題です。
(例題1)
\(xyz\)空間において、平面 \(z=0\) 上の原点を中心とする半径\(2\)の円を底面とし、点\((0,0,1)\) を頂点とする円錐を\(A\)とする。
次に、平面 \(z=0\) 上の点 \((1,0,0)\) を中心とする半径\(1\)の円を\(H\)、平面 \(z=1\) 上の点 \((1,0,1)\) を中心とする半径\(1\)の円を\(K\)とする。\(H\)と\(K\)を2つの底面とする円柱を\(B\)とする。
円錐\(A\)と円柱\(B\)の共通部分を\(C\)とする。
\(0≦t≦1\) を満たす実数\(t\)に対し、平面 \(z=t\) による\(C\)の切り口の面積を\(S(t)\)とおく。
(1)\(0≦θ≦\displaystyle\frac{π}{2}\) とする。\(t=1-\cosθ\) のとき、\(S(t)\)を\(θ\)で表せ。
(2)\(C\)の体積 \(\displaystyle\int_{0}^{1}S(t)dt\) を求めよ。
(解答)
(1)
円錐の断面も円柱の断面もどちらも円なので、共通部分は2円が重なっている部分になります。よって共通部分の面積を求めるのには、扇形などの面積を求める必要があるので角\(θ\)の情報が必要になってきます。これが問題文で \(t=1-\cosθ\) で与えられているので、この\(θ\)が \(z=t\) のときの図で一体どの角を表しているかを探す必要があります。
円柱の断面は常に一定なので、まず円錐の断面が \(z=t\) でどのような円になるかを調べていきます。
円柱\(B\)の \(z=t\) による断面は、\(Q(1,0,t)\) を中心とする半径\(1\)の円。(\(z=t\) 上の\(xy\)平面では \((1,0)\) を中心とする半径\(1\)の円)
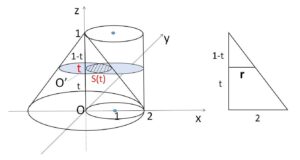
円錐\(A\)の断面については、中心が \(O'(0,0,t)\) の円 (\(t=1\) のときは頂点の1点)。
半径\(r\)は、\(O’\)が原点\(O\)と円錐の頂点を結ぶ線分を \(t:1-t\) に内分していることから
\(r=2(1-t)=2\cosθ\)
\(z=t\) による2つの立体の共通部分の断面は、この2円の共通部分である。
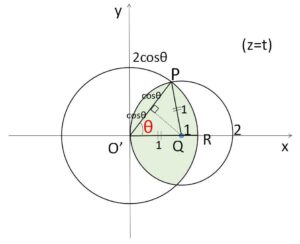
図の\(△O’PQ\)は二等辺三角形で、\(O’Q=PQ=1\) と \(O’P=2\cosθ\) より
\(\angle QO’P=θ\) である。
断面図は\(y\)軸について対称で、\(\angle PQO’=π-2θ\) より
\(S(t)=2\{扇形QPO’+(扇形O’PR-△O’PQ)\}\)
\(=2\left\{\displaystyle\frac{1}{2}\cdot1^2\cdot(π-2θ)+\displaystyle\frac{1}{2}\cdot(2\cosθ)^2\cdotθ-\displaystyle\frac{1}{2}\cdot1\cdot2\cosθ\cdot\sinθ\right\}\)
\(=π-2θ+4θ\cos^2θ-2\sinθ\cosθ\)
(参考)
\(θ\)がどの角を表しているかは、次のように判断することも可能です。
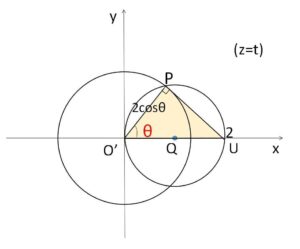
\(O’U=2\) (右側の円の直径) で、直径に対する円周角だから \(\angle O’PU=\displaystyle\frac{π}{2}\)。よって \(O’P=2\cosθ\) より、\(\angle UO’P=θ\) と決定できます。
(2)
\(t=1-\cosθ\) より \(dt=\sinθdθ\)
(\(0≦θ≦\displaystyle\frac{π}{2}\) )
よって体積\(V\)は
\(V=\displaystyle\int_{0}^{1}S(t)dt\)
(積分範囲の対応に注意)
\(=\displaystyle\int_{0}^{\frac{π}{2}}(π-2θ+4θ\cos^2θ-2\sinθ\cosθ)\sinθdθ\)
\(=\displaystyle\int_{0}^{\frac{π}{2}}(π\sinθ-2θ\sinθ+4θ\cos^2θ\sinθ-2\sin^2θ\cosθ)dθ\)
ここで
\(I_1=\displaystyle\int_{0}^{\frac{π}{2}}π\sinθdθ=π[-\cosθ]_{0}^{\frac{π}{2}}=π\)
\(I_2=\displaystyle\int_{0}^{\frac{π}{2}}2θ\sinθdθ=[2θ(-\cosθ)]_{0}^{\frac{π}{2}}+\displaystyle\int_{0}^{\frac{π}{2}}2\cosθdθ\)
\(=0+2[\sinθ]_{0}^{\frac{π}{2}}=2\)
\(I_3=\displaystyle\int_{0}^{\frac{π}{2}}4θ\cos^2θ\sinθdθ\) (\(4θ\)の\(θ\)を消すように部分積分する)
\(=\left[4θ(-\displaystyle\frac{\cos^3θ}{3})\right]_{0}^{\frac{π}{2}}+\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{4}{3}\cos^3θdθ\)
\(=0+\displaystyle\frac{4}{3}\displaystyle\int_{0}^{\frac{π}{2}}(1-\sin^2θ)\cosθdθ\)
\(=\displaystyle\frac{4}{3}\left[\sinθ-\displaystyle\frac{1}{3}\sin^3θ\right]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{8}{9}\)
\(I_4=\displaystyle\int_{0}^{\frac{π}{2}}2\sin^2θ\cosθdθ=\left[\displaystyle\frac{2}{3}\sin^3θ\right]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{2}{3}\)
となるから、
\(V=I_1-I_2+I_3-I_4\)
\(=π-2+\displaystyle\frac{8}{9}-\displaystyle\frac{2}{3}\)
\(=π-\displaystyle\frac{16}{9}\)
(例題2)
\(xyz\)空間に5点 \(A(1,1,0)\)、\(B(-1,1,0)\)、\(C(-1,-1,0)\)、\(D(1,-1,0)\)、\(P(0,0,3)\) をとる。四角錐\(PABCD\)の \(x^2+y^2≧1\) みたす部分の体積を求めよ。
\(x^2+y^2=1\) (円柱の側面) の断面は半径\(1\)の円で固定で、四角錐の断面は上部にいくほど小さくなっていきます。よって\(t\)の範囲は頂点の\(z\)座標\(3\)までではなく、途中で円の内部にすっぽりと正方形が入り込むところまでになり、この場合の\(t\)の値を求める必要があります。
また、図形の対称性も利用していきます。
(解答)
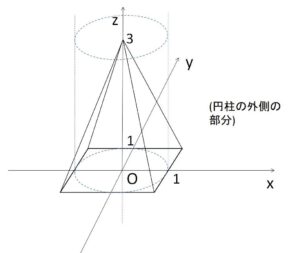
\(z=t\) による断面を考える。
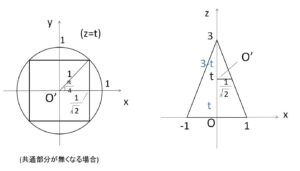
まず、四角錐の断面である正方形が円柱の断面である円に内接するときの\(t\)の値を求める。そのときの正方形の1辺長さの半分は\(\displaystyle\frac{1}{\sqrt{2}}\)。よって\(xz\)平面での相似形より
\(1:3=\displaystyle\frac{1}{\sqrt{2}}:(3-t)\)
よって、\(t=3(1-\displaystyle\frac{1}{\sqrt{2}})\) となるので
\(0≦t≦3(1-\displaystyle\frac{1}{\sqrt{2}})\)・・・①
の範囲で題意の立体の断面が存在することになる。
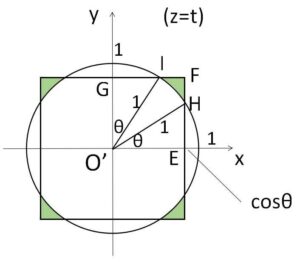
①の範囲において、\(z=t\) による断面は上図のようになり、角\(θ\)を図のように設定すると対称性から題意の立体の断面積\(S(t)\)は
\(S(t)=4(正方形O’EFG-2△O’EH-扇形O’HI)\)
\(=4\left\{\cos^2θ-2\cdot\displaystyle\frac{1}{2}\cosθ\sinθ-\displaystyle\frac{1}{2}\cdot1^2\cdot(\displaystyle\frac{π}{2}-2θ)\right\}\)}
\(=4\left(\cos^2θ-\cosθ\sinθ+θ-\displaystyle\frac{π}{4}\right)\)
(置換積分用に、\(t\)と\(θ\)の関係式を求めます。最初と同様に\(xz\)平面の相似を考えればよいです)
また、先ほどと同様に\(xz\)平面による相似形を考えると
\(1:3=\cosθ:(3-t)\) だから
\(t=3-3\cosθ\)・・・②
①の範囲内での\(θ\)の範囲は②より
\(0≦θ≦\displaystyle\frac{π}{4}\)
したがって \(dt=3\sinθdθ\) より、求める体積\(V\)は
\(V=\displaystyle\int_{0}^{3(1-\frac{1}{\sqrt{2}})}S(t)dt\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}4\left(\cos^2θ-\cosθ\sinθ+θ-\displaystyle\frac{π}{4}\right)\cdot3\sinθdθ\)
\(=12\displaystyle\int_{0}^{\frac{π}{4}}\left(\cos^2θ\sinθ-\sin^2θ\cosθ+θ\sinθ-\displaystyle\frac{π}{4}\sinθ\right)dθ\)
(\(\displaystyle\intθ\sinθdθ=-θ\cosθ+\displaystyle\int\cosθdθ=-θ\cosθ+\sinθ+C\) より)
\(=12\left[-\displaystyle\frac{1}{3}\cos^3θ-\displaystyle\frac{1}{3}\sin^3θ-θ\cosθ+\sinθ+\displaystyle\frac{π}{4}\cosθ\right]_{0}^{\frac{π}{4}}\)
\(=12\left\{(-\displaystyle\frac{1}{3\cdot2\sqrt{2}}×2-\displaystyle\frac{π}{4\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{π}{4\sqrt{2}})-(-\displaystyle\frac{1}{3}+\displaystyle\frac{π}{4})\right\}\)
\(=12\left(\displaystyle\frac{2}{3\sqrt{2}}+\displaystyle\frac{1}{3}-\displaystyle\frac{π}{4}\right)\)
\(=4\sqrt{2}+4-3π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→通過領域と体積 back→空間の回転③(立体図形の回転)