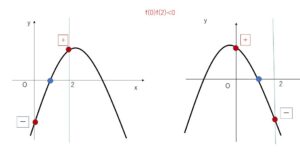
2次方程式の2実数解のうち、ただ1つのみがある区間にある条件を考えていきます。→(8-3)2つの区間に1つずつの解 で紹介した性質を使いますが少し注意が必要です。
(問題)
\(x\)の2次方程式、\(-2x^2+kx+k^2+5=0\) が2つの異なる解をもち、そのうちの1つだけが \(0<x<2\) の範囲にある。このとき定数\(k\)の値の範囲を求めよ。
左辺を\(f(x)\)とおくと、\(f(0)f(2)<0\) を使いますが、\(f(0)=0\) または \(f(2)=0\) の場合でも題意を満たす可能性があるので検討する必要があります。例えば、\(f(0)=0\)でもう1つの解\(α\)が \(0<x<2\) の範囲にあれば、方程式の2解は, \(x=0,α\) となり、\(0<α<2\)から題意を満たすことになります。\(f(2)=0\) の場合も同様です。
(解答)
\(f(x)=-2x^2+kx+k^2+5\) とおくと、\(y=f(x)\)が\(x\)軸と \(0<x<2\) の範囲でただ1つの交点をもつ条件を考えればよい。
①\(f(0)f(2)<0\)のとき
\((k^2+5)(k^2+2k-3)<0\) \(k^2+5>0\)だから
\(k^2+2k-3<0\) となり \((k+3)(k-1)<0\) より
\(-3<k<1\)
\(k^2+2k-3<0\) となり \((k+3)(k-1)<0\) より
\(-3<k<1\)
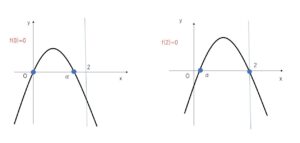
②\(f(0)=0\)のときは \(f(0)=k^2+5>0\)より存在しない。
\(f(2)=0\) のとき \(k=-3,1\)であり、
\(k=-3\)ならば 2次方程式は \(2x^2+3x-14=0\)であり
\((2x+7)(x-2)=0\) より 解は \(x=-\displaystyle\frac{7}{2},2\) となるので題意を満たさない。
\(k=1\) ならば 2次方程式は \(2x^2-x-6=0\) であり
\((2x+3)(x-2)=0\) より 解は \(x=-\displaystyle\frac{3}{2},2\) となるので題意を満たさない。
\(f(2)=0\) のとき \(k=-3,1\)であり、
\(k=-3\)ならば 2次方程式は \(2x^2+3x-14=0\)であり
\((2x+7)(x-2)=0\) より 解は \(x=-\displaystyle\frac{7}{2},2\) となるので題意を満たさない。
\(k=1\) ならば 2次方程式は \(2x^2-x-6=0\) であり
\((2x+3)(x-2)=0\) より 解は \(x=-\displaystyle\frac{3}{2},2\) となるので題意を満たさない。
以上①②より求める\(k\)の範囲は
\(-3<k<1\)
\(-3<k<1\)
結局、\(f(0)=0\) または \(f(2)=0\) の場合は問題文の条件を満たさないわけですが、この検討は必ずしてください。
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。