線分上を動く点に関する軌跡・領域の例題です。
(例題)
複素数平面上の原点以外の点\(z\)に対して
\(w=\displaystyle\frac{1}{z}\)
とする。\(1\)の3乗根のうち虚部が正であるものを\(β\)とし、点\(β\)と点\(β^2\)を結ぶ線分上を点\(z\)が動くとき、点\(w\)の軌跡を求めよ。
(i)\(x+yi\) とおく方法(実数平面で考える)
(ii)円の内部の不等式を利用する方法(複素数のまま考える)
があります。
(解答1)
\(t^3=1\) の虚数解は
\(t=\displaystyle\frac{-1±\sqrt{3}i}{2}\) だから
\(β=-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\)、\(β^2=-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
\(z=x+yi\) (\((x,y)≠(0,0)\)) とおくと、\(z\)が\(β,β^2\)を結ぶ線分上を動くことから
\(x=-\displaystyle\frac{1}{2}\)
\(y=k\) (\(-\displaystyle\frac{\sqrt{3}}{2}≦k≦\displaystyle\frac{\sqrt{3}}{2}\))
(あとは媒介変数\(k\)の軌跡の問題になります)
このとき上記\(x,y\)では \((x,y)≠(0,0)\) を満たし
\(w=\displaystyle\frac{1}{z}\)
\(=\displaystyle\frac{1}{-\displaystyle\frac{1}{2}+ki}\)\(=\displaystyle\frac{-\displaystyle\frac{1}{2}-ki}{\displaystyle\frac{1}{4}+k^2}\)
\(=-\displaystyle\frac{2}{4k^2+1}-\displaystyle\frac{4k}{4k^2+1}i\)
よって \(w=X+Yi\) とおけば
\(X=-\displaystyle\frac{2}{4k^2+1}\)・・・①
\(Y=-\displaystyle\frac{4k}{4k^2+1}\)・・・②
\(-\displaystyle\frac{\sqrt{3}}{2}≦k≦\displaystyle\frac{\sqrt{3}}{2}\) だから①より
\(-\displaystyle\frac{2}{4\cdot0^2+1}≦X≦-\displaystyle\frac{2}{4\cdot(±\displaystyle\frac{\sqrt{3}}{2})^2+1}\)
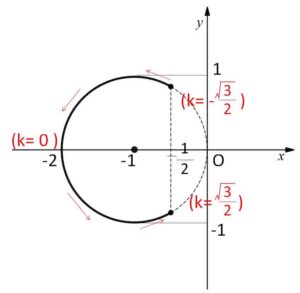
\(-2≦X≦-\displaystyle\frac{1}{2}\)
また②より
\(\displaystyle\frac{dY}{dk}=-4\cdot\displaystyle\frac{(4k^2+1)-k\cdot8k}{(4k^2+1)^2}\)
\(=\displaystyle\frac{4(4k^2-1)}{(4k^2+1)^2}\)
\(k=±\displaystyle\frac{1}{2},±\displaystyle\frac{\sqrt{3}}{2}\) での\(Y\)の値を調べることにより
\(-1≦Y≦1\)
\(X=-\displaystyle\frac{2}{4k^2+1}\)・・・①
\(Y=-\displaystyle\frac{4k}{4k^2+1}\)・・・②
において①を②に代入すると
\(Y=-2kX\)
①より \(X≠0\) だから
\(k=-\displaystyle\frac{Y}{2X}\)・・・③
③を①に代入して
\(X=-\displaystyle\frac{2}{4(-\displaystyle\frac{Y}{2X})^2+1}\)
\(1=-\displaystyle\frac{2X}{Y^2+X^2}\)
したがって
\((X+1)^2+Y^2=1\)・・・④
以上より\(w\)の軌跡は円④の \(X≦-\displaystyle\frac{1}{2}\) の部分になる。
(解答2)
2点\(β,β^2\)を通る直線(実部が\(-\displaystyle\frac{1}{2}\))は、点\(-1,0\)を結ぶ線分の垂直2等分線。このうち\(β,β^2\)を結ぶ線分は、原点を中心とする半径\(1\)の円の内部です(円によって直線を切り取るイメージ)。この2つの条件を\(z\)で表せば、あとはいつものように \(w=\displaystyle\frac{1}{z}\) から\(z\)を消去すればよいです。
(\(β,β^2\)を通る直線については、共役複素数を使って実部が\(-\displaystyle\frac{1}{2}\) として立式してもよいです)
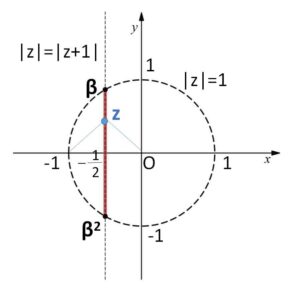
2点\(β,β^2\)を結ぶ線分は、2点\(β,β^2\)を通る直線のうち原点\(O\)を中心とする半径\(1\)の円の内部なので、この線分は次のように表される。
\(|z|=|z+1|\)・・・(i)
かつ
\(|z|≦1\)・・・(ii)
\(w=\displaystyle\frac{1}{z}\) より
\(z=\displaystyle\frac{1}{w}\)・・・(iii) (\(w≠0\))
なので、(iii)を(i)(ii)に代入すると
(i)について
\(\left|\displaystyle\frac{1}{w}\right|=\left|\displaystyle\frac{1}{w}+1\right|\)
\(\left|\displaystyle\frac{1}{w}\right|=\left|\displaystyle\frac{1+w}{w}\right|\)
よって
\(|w+1|=1\)
(ii)について
\(\left|\displaystyle\frac{1}{w}\right|≦1\) より
\(|w|≧1\)
したがって
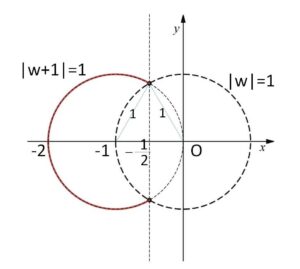
\(|w+1|=1\) かつ \(|w|≧1\) かつ \(w≠0\)
が\(w\)の軌跡であり、図示すると次のようになる。(点\(-1\)を中心とする半径\(1\)の円周のうち、原点を中心とする半径\(1\)の円の外側)
(参考)
直線の方程式を(i)の代わりに
\(\displaystyle\frac{z+\bar{z}}{2}=-\displaystyle\frac{1}{2}\)
とすると
\(z+\bar{z}=-1\) より
\(\displaystyle\frac{1}{w}+\displaystyle\frac{1}{\bar{w}}=-1\) (ただし\(w≠0\))
\(\bar{w}+w=-w\bar{w}\)
\((w+1)(\bar{w}+1)=1\)
\(|w+1|^2=1\)
\(|w+1|=1\)
となり、同じ円の方程式が得られる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数平面の軌跡・領域の図形的解法 back→複素数平面と領域②(x+yi型)