中線定理について見ていきます。
・中線定理
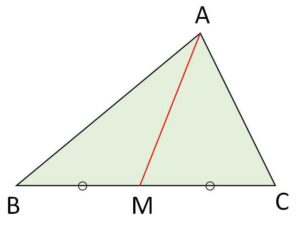
\(△ABC\)において、辺\(BC\)の中点を\(M\)とすると
\(AB^2+AC^2=2(AM^2+BM^2)\)
(\(BM=CM\))
(解説)
中線\(AM\)に関する定理です。証明は座標平面を使うと(\(M\)を原点にとるとよい)、とても楽に示せますが、今回は敢えて図形のままで証明したいと思います。(三平方の定理を主に使う)
(証明)
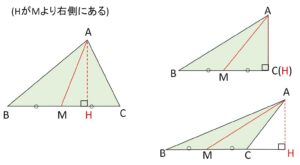
\(A\)から\(BC\)に垂線\(AH\)を下ろす。
\(H\)が\(M\)より右側について考える。(左側、\(H,M\)が一致する場合も同様に示せる)
\(AB^2+AC^2\)
\(=(BH^2+AH^2)+(CH^2+AH^2)\)
\(=(BM+MH)^2+(CM-MH)^2+2AH^2\)
(展開して \(BM=CM\) より)
\(=2BM^2+2MH^2+2AH^2\)
\(=2BM^2+2(MH^2+AH^2)\)
\(=2BM^2+2AM^2\)
(例題)
平行四辺形\(ABCD\)において、次の等式が成り立つことを証明せよ。
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2\)
(解答)
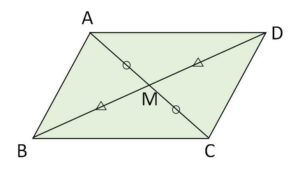
対角線の交点を\(M\)とすると
\(AM=CM\)、\(BM=MD\)・・・①
\(△ABD\)において中線定理より
\(AB^2+DA^2=2(AM^2+BM^2)\)・・・②
同様に\(△CBD\)において
\(BC^2+CD^2=2(CM^2+BM^2)\)・・・③
②+③より、①も用いると
\(AB^2+BC^2+CD^2+DA^2=4AM^2+4BM^2\)
また①より
\(AC=2AM\)、\(BD=2BM\)
だから
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積比 back→三角形の3辺の大小(例題)