平面上の最短距離(直線図形)について見ていきます。
・最短距離と直線図形
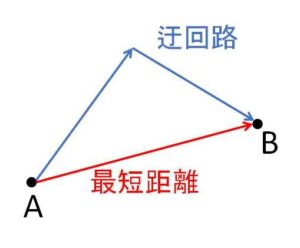
平面上での最短距離は、2点間を結ぶ線分に着目するのが基本です。上図で\(A\)から\(B\)への行き方は無数に存在しますが、最短になるような経路は\(AB\)を直線で結ぶ経路です。(三角不等式を使えばよい)
最短経路(円以外の直線図形)の基本パターンとしては次の通りです。
(対称移動型)
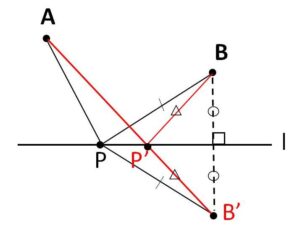
\(A,B\)は固定された点で、直線\(l\)上を\(P\)が動くとします。\(A \to P \to B\) と進む経路で最も短いものを探すには、\(B\)(\(A\)でもよい)を\(l\)について対称移動させればよいです。すると元々\(l\)について同じ側にあった\(A,B\)が反対側に位置するので折れ線を解消できます。つまり
\(AP+PB=AP+PB’\)
より、\(A,B’\)の最短経路を考えればよく、線分\(AB’\)と\(l\)の交点を\(P’\)とすれば\(A \to P’ \to B\)が最短経路になります。
(平行移動型)
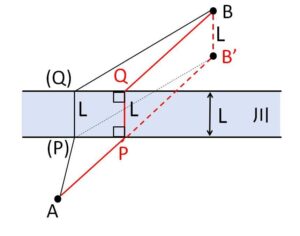
\(A,B\)は固定された点で、図の川を渡るときは川岸に垂直に移動しなければならないとして、\(A \to B\)の最短経路を考えます。垂直方向の移動は必ずしなければならないので、\(B\)からその分\(L\)だけ平行移動した点を\(B’\)とします。そうすると\(A,B’\)の移動を考えればよくなります。川を渡る箇所の川岸を\(P,Q\)とすれば、四角形\(PQBB’\)は平行四辺形になるので
\(AP+PQ+QB=AP+L+PB’\)
より、\(A,P,B’\)が一直線上にあれば\(AP+PB’\)は最小となるので、図の赤色の経路\(A \to P \to Q \to B\)が最短経路になります。
(\(A\)を平行移動してもよいです)
(例題)
図のような \(\angle A=60°\) の鋭角三角形\(ABC\)がある。辺\(BC\)上に点\(P\)、辺\(AB,AC\)上に点\(Q,R\)があるとする。
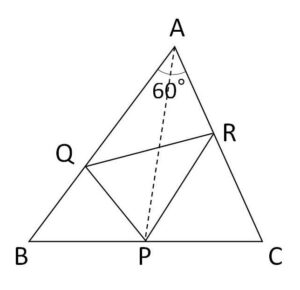
(1)点\(P\)は定点、点\(Q,R\)は辺上を動く動点とする。\(AP=6\) のとき\(△PQR\)の周長の最小値を求めよ。
(2)点\(P\)も動点とするとき、\(△PQR\)の周長が最小となるときの点\(P,Q,R\)の位置を求めよ。
(解答)
(1)
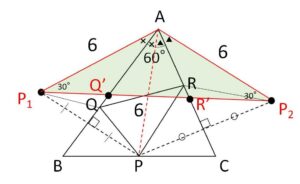
\(P\)の\(AB,AC\)に対する対称な点を\(P_1,P_2\)とする。
\(PQ+QR+RP=P_1Q+QR+RP_2\)
となるから、周長が最小となるとき\(P_1,Q,R,P_2\)が一直線上にある。(図の\(Q’,R’\))・・・(注)
\(△AP_1P_2\)において ×+▲=60° だから、\(P_1,P_2\)が\(P\)の対称点であることに着目すると
\(\angle P_1AP_2=120°\)、\(AP_1=AP_2=6\)
周長の最小値は\(P_1P_2\)の長さだから余弦定理より・・・(注)
\(P_1P_2=\sqrt{6^2+6^2-2\cdot6\cdot6\cdot\cos120°}\)
\(=6\sqrt{3}\)
(注)
動点が\(Q,R\)の2つですが、片方\(R\)を固定すると経路を小さくするには
「\(P_1,Q,R\)が一直線上」
となるようにすればよく(\(R\)を決めれば\(Q\)は\(P_1R\)上の点に決まる)、さらに\(R\)を動すとき
「\(P_1,R,P_2\)が一直線上」
となるようにすればよいので、4点が一直線上にあることになります。
また、余弦定理を使わなくても\(A\)から\(P_1P_2\)に垂線を下ろせば、\(30°,60°,90°\)の直角三角形を2つ合わせた形になることから、\(P_1P_2\)の長さを求めることができます。
(2)
\(x\)を小さくすれば周長が小さくなるので、\(AP\)は垂線になることが分かります。今、\(P\)を最初に固定して動かすという方法をとっていますが、他の点\(Q,R\)でも同じことが言えるはずです。
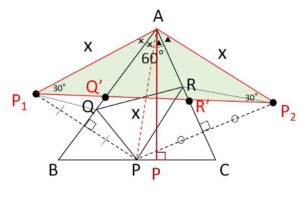
\(AP=x\) とすると(1)と同様に考えて周長の最小値は
\(P_1P_2=\sqrt{3}x\)
となる。よって\(x\)が最小値をとるとき周長は最小値となるので、このとき\(AP\)は\(BC\)に対する垂線となり、\(Q,R\)は1通りに決定される。
ここで、\(Q\)または\(R\)を最初に固定しても同様の結果が得られるため、\(CQ\)も\(BR\)も、それぞれ\(AB,AC\)に対する垂線となる。
よって、\(P,Q,R\)の位置は頂点\(A,C,B\)から対辺に下ろした垂線の足になる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→折り返しと平面図形 back→面積比