球の性質

球に関する事項についてまとめます。

・球の性質
球は円を回転してできた立体で対称性が強いので、様々な性質をもちます。

(解説)
(1)

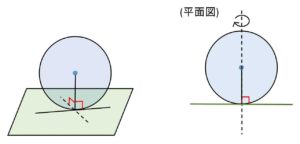
平面の場合の円と直線の関係に対応するのが、この空間における球と平面の関係です。球の中心と接点を結ぶ直線が平面に垂直なのは、平面で円と接線を考えた場合を回転させると、円が球になり直線が垂直を満たしながら平面になることから分かります。

(2)

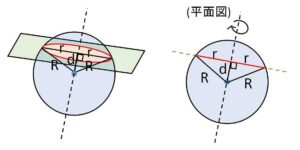
同様に平面図を回転させると分かります。特に切断する平面が球の中心を通るとき断面の円の半径は最大になり、大円の半径は球の半径\(R\)と同じです。その他の小円の半径\(r\)については三平方の定理より
\(R^2=r^2+d^2\)　(\(d\)は球の中心と円の中心の距離)
が成り立つことから求めます。

・2つの球の位置関係
2つの球(球面とする)の位置関係については、円の場合と同様です。
2つの球の半径を\(R,R’\ (r>r’)\)とし、中心間距離を\(d\)とすると

(1)\(d>R+R’\): 外部にある (共有点なし)
(2)\(d=R+R’\): 外接する(1点で交わる)
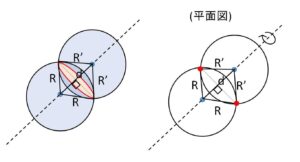
(3)\(R-R'<d<R+R’\): 無数の点で交わる(共有部分は円)
(4)\(d=R-R’\): 内接する(1点で交わる)
(5)\(d<R-R’\): 内部にある (共有点なし)

(3)についですが、平面において2点で交わる円(円周のみ)を回転させることで、共通部分が円になることが分かります(下図)。また(2)(4)の接する場合に、中心を結ぶ直線上に接点があるのは円と同じですが、これも接する2円の回転を考えれば分かります。

・外接球・内接球
ある立体に外側で接する球である外接球、内側で接する球である内接球の問題では球の中心を通る平面を取り出して、平面図で考えるのが基本です。例えば四面体では、外接球は4頂点を通る球で、内接球は4面に接する球です。ただし、内接球の場合では円の内接円の場合と同様に、立体を分けて (全体の体積)=(分割した立体の和) より内接球の半径を計算で求めることも可能です。
また他にも、立体の辺に接する球も存在する場合があり、これも断面図により処理していくことになります。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→接する複数の球　back→等面四面体