・三角形の成立条件
三角形の3辺の大きさはどのような値でもよいのでしょうか。答えは否で、例えば \(1,1,100\) を3辺にもつ三角形は存在しないこと分かるでしょう。三角形が存在する条件、つまり三角形の成立条件を一般的に数式で表すには「三角形の1辺の長さは他の2辺の和より小さい」ことを利用します。「」内を数式で表すと
\(a<b+c\)・・・① かつ \(b<c+a\)・・・② かつ \(c<a+b\)・・・③
です。②は \(b-c<a\), ③は\(c-b<a\) となるので、②③をまとめると
\(|b-c|<a\) であり、①と合わせると
\(|b-c|<a<b+c\) となります。これが三角形の成立条件です。
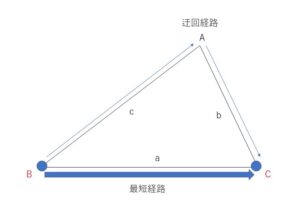
「三角形の1辺の長さは他の2辺の和より小さい」ことは、2点を結ぶ経路は、2点を結ぶ線分が最小であることから分かります。例えば点\(B,C\)の場合では、最短経路は線分\(BC\)つまり\(a\)で、迂回する経路\(BA+AC\)は\(c+b\)なので、\(a<b+c\) となります。

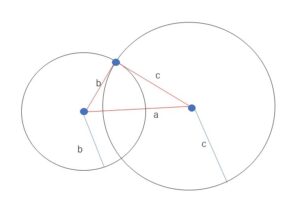
今、三角形が成立するならば\(|b-c|<a<b+c\)が成り立つことが分かったので、逆に、\(|b-c|<a<b+c\)が成り立てば三角形が存在することが分かれば、必要十分条件となります。「\(|b-c|<a<b+c\) → 三角形が存在する」を示すには、半径\(b,c\)の円を中心間距離\(a\)として配置すれば、条件から2円は2点で交わり、2つの円の中心(計2点)と円の交点のうち1つを頂点とする三角形が存在することがわかります。この三角形の3辺は\(a,b,c\)です。
※\(a,b,c\)が正の値になることは下の例題の解説に載せてあります。
・辺と角の大小関係①
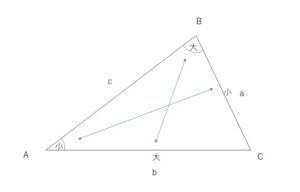
三角形の2辺の大小関係とその対角の大小関係は一致します。つまり大きい辺の対角のほうが大きく、また大きい角の対辺のほうが大きくなります。
三角形の2辺の大小関係とその対角の大小関係は一致します。つまり大きい辺の対角のほうが大きく、また大きい角の対辺のほうが大きくなります。
\(a<b\) \(\leftrightarrow\) \(A<B\)
\(a=b\) \(\leftrightarrow\) \(A=B\)
\(a>b\) \(\leftrightarrow\) \(A>B\)
(証明)
\(a<b\) \(\leftrightarrow\) \(A<B\) について証明する。
\(a<b\) \(\leftrightarrow\) \(A<B\) について証明する。
\(\cos A-\cos B=\displaystyle\frac{b^2+c^2-a^2}{2bc}-\displaystyle\frac{c^2+a^2-b^2}{2ca}\)
\(=\displaystyle\frac{ab^2+ac^2-a^3-(bc^2+a^2b-b^3)}{2abc}\)
(分子)\(=ab(b-a)+c^2(a-b)+(b-a)(b^2+ab+a^2)\)
\(=(b-a)\{(b+a)^2-c^2\}\)
\(=(b-a)(a+b+c)(a+b-c)\)
\(=(b-a)\{(b+a)^2-c^2\}\)
\(=(b-a)(a+b+c)(a+b-c)\)
\(a+b+c>0\), \(a+b-c>0\) (三角形の成立条件から), \(abc>0\) なので
\(a<b\) \(\leftrightarrow\) \(\cos A>\cos B\) \(\leftrightarrow\) \(A<B\)
他の2つも同様に示される。
三角比と角の大小対応が分かりやすい\(\cos\)について検討しました(ただし角が大きいほど三角比は小さくなることに注意)。\(\sin\)だと三角比の大小と角の大小は必ずしも一致しません。(例 \(\sin30°<\sin120°\) \(\sin150°<\sin60°\)のようにバラバラ)
・辺と角の大小関係②
三角形の角の大きさと辺の長さの2乗について次の関係が成り立ちます。
三角形の角の大きさと辺の長さの2乗について次の関係が成り立ちます。
\(A<90°\) \(\leftrightarrow\) \(a^2<b^2+c^2\)
\(A=90°\) \(\leftrightarrow\) \(a^2=b^2+c^2\)
\(A>90°\) \(\leftrightarrow\) \(a^2>b^2+c^2\)
(証明)
\(\cos A =\displaystyle\frac{b^2+c^2-a^2}{2bc}\) より
\(A<90°\) \(\leftrightarrow\) \(\cos A >0\) \(\leftrightarrow\) \(a^2<b^2+c^2\)
\(A=90°\) \(\leftrightarrow\) \(\cos A =0\) \(\leftrightarrow\) \(a^2=b^2+c^2\)
\(A>90°\) \(\leftrightarrow\) \(\cos A <0\) \(\leftrightarrow\) \(a^2>b^2+c^2\)
\(A=90°\) \(\leftrightarrow\) \(\cos A =0\) \(\leftrightarrow\) \(a^2=b^2+c^2\)
\(A>90°\) \(\leftrightarrow\) \(\cos A <0\) \(\leftrightarrow\) \(a^2>b^2+c^2\)
\(A=90°\) の場合は三平方の定理そのものです。
(例題)
\(x+1,x+2,x+3\) が鈍角三角形の3辺となるような\(x\)の値の範囲を求めよ。
まず、三角形が存在する条件から調べます。
\(|b-c|<a<b+c\) をそのまま使ってもよいですが、\(a\)が最大辺の場合、\(|b-c|<a\) は必ず成り立つので、\(a<b+c\) のみを用います。
(\(|b-c|<a\) は \(b-c<a\) かつ \(c-b<a\) なので、\(a\)が最大辺の場合は明らかに成り立ちます)
また、\(|b-c|<a<b+c\)・・・(※) が成り立つとき、\(|b-c|<a\) より \(a>0\)となり、(1)\(b≧c\) のとき (※)から \(b-c<b+c\) よって\(c>0\)
\(b≧c\) から \(b>0\) となる。(2)\(b<c\)のときも同様に、\(b>0,c>0\)となる。要するに(※)が成り立つときは \(a,b,c\)は全て正の数になることが保証されているということです。
\(a\)が最大辺の場合、\(|b-c|<a\) は必ず成り立つので、\(a<b+c\) のみで\(a,b,c\)は正の数となります。
よって、辺の長さが正になるかどうかは調べなくてよいです。
\(|b-c|<a<b+c\) をそのまま使ってもよいですが、\(a\)が最大辺の場合、\(|b-c|<a\) は必ず成り立つので、\(a<b+c\) のみを用います。
(\(|b-c|<a\) は \(b-c<a\) かつ \(c-b<a\) なので、\(a\)が最大辺の場合は明らかに成り立ちます)
また、\(|b-c|<a<b+c\)・・・(※) が成り立つとき、\(|b-c|<a\) より \(a>0\)となり、(1)\(b≧c\) のとき (※)から \(b-c<b+c\) よって\(c>0\)
\(b≧c\) から \(b>0\) となる。(2)\(b<c\)のときも同様に、\(b>0,c>0\)となる。要するに(※)が成り立つときは \(a,b,c\)は全て正の数になることが保証されているということです。
\(a\)が最大辺の場合、\(|b-c|<a\) は必ず成り立つので、\(a<b+c\) のみで\(a,b,c\)は正の数となります。
よって、辺の長さが正になるかどうかは調べなくてよいです。
(解答)
最大辺は\(x+3\)なので、三角形が成立する条件は
\(x+3<(x+1)+(x+2)\)
これを解くと、\(x>0\)・・・①
最大辺は\(x+3\)なので、三角形が成立する条件は
\(x+3<(x+1)+(x+2)\)
これを解くと、\(x>0\)・・・①
また三角形が鈍角三角形になるとき、最大の辺の対角が鈍角になることから
\((x+3)^2>(x+2)^2+(x+1)^2\)
これを解くと、\(-2<x<2\) ・・・②
\((x+3)^2>(x+2)^2+(x+1)^2\)
これを解くと、\(-2<x<2\) ・・・②
①②から \(0<x<2\)
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。