正多角形の面積を三角比を用いて求めてみます。ポイントは分割された三角形と円です。
(例題1)
半径1の円に内接する正十二角形の面積を求めよ。
図示するには、円周を12等分する点をそれぞれとります。弧の長さと弦の長さは比例するので 同じ長さの弧に対応する弦の長さは等しいので、12等分した点を結ぶと全ての辺が等しい十二角形ができます。また、円の中心を通る対角線で十二角形を12個の三角形に分割すると、どの三角形も2辺が円の半径で、挟まれる角は円周を12等分したことから\(360°÷12=30°\)となり、すべての三角形は合同となります。よって十二角形の内角は全て等しく、正十二角形になります。
(解答)
半径1の円に内接する正十二角形は図示すると次の通り。
半径1の円に内接する正十二角形は図示すると次の通り。
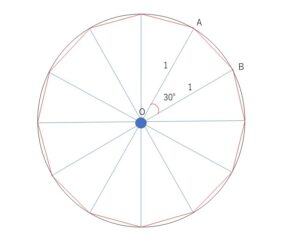
正十二角形を円の中心を通る対角線で分割すると、12個の三角形はすべて合同な三角形となる。
図のように3点\(O,A,B\)をとると、\(\angle AOB=360°÷12=30°\)
\(OA=OB=1\) だから
求める面積\(S\)は
図のように3点\(O,A,B\)をとると、\(\angle AOB=360°÷12=30°\)
\(OA=OB=1\) だから
求める面積\(S\)は
\(S=12×\displaystyle\frac{1}{2}・1・1・\sin30°=\)\(3\)
(例題2)
一辺の長さが\(1\)の正十二角形の面積を求めよ。
円と正十二角形を描きます。円の中心を通る対角線で12等分された三角形は、長さ1以外の2辺は円の半径、その2辺に挟まれる角は30°となります。余弦定理により2辺を求めます。
(解答)
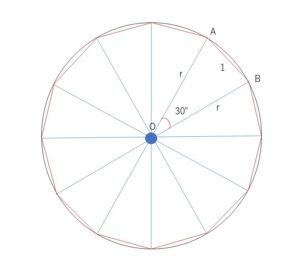

図は正十二角形とそれに外接する円であり、円の中心を通る対角線で12分割すると、すべての三角形は合同となる。図のように3点\(O,A,B\)をとると
\(\angle AOB=360°÷12=30°\)また、\(OA=OB=r\) とおくと、余弦定理より
\(1^2=r^2+r^2-2r・r\cos30°\)
整理すると
\((2-\sqrt{3})r^2=1\) となり
\(r^2=\displaystyle\frac{1}{2-\sqrt{3}}=\displaystyle\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}=2+\sqrt{3}\)
\(\angle AOB=360°÷12=30°\)また、\(OA=OB=r\) とおくと、余弦定理より
\(1^2=r^2+r^2-2r・r\cos30°\)
整理すると
\((2-\sqrt{3})r^2=1\) となり
\(r^2=\displaystyle\frac{1}{2-\sqrt{3}}=\displaystyle\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}=2+\sqrt{3}\)
したがって求める面積\(S\)は
\(S=12×\displaystyle\frac{1}{2}・r・r・\sin30°=3r^2=\)\(6+3\sqrt{3}\)
\(S=12×\displaystyle\frac{1}{2}・r・r・\sin30°=3r^2=\)\(6+3\sqrt{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。