三角形の面積の最小値に関する問題について考えていきます。
(問題)
1辺の長さが\(1\)の正三角形の辺\(AB,BC,CA\)上にそれぞれ点\(D,E,F\)をとり、
\(AD=x,BE=2x,CF=3x\)とする。
(1)\(△DEF\)の面積\(S\)を\(x\)で表せ。
(2)(1)の面積を最小にする\(x\)の値と最小値を求めよ。
\(△DEF\)を直接求めるのは大変そうなので、求めやすい\(△ADF,△DBE,△ECF\)を求めて全体の三角形\(ABC\)から引いてやります。
(解答)
(1)
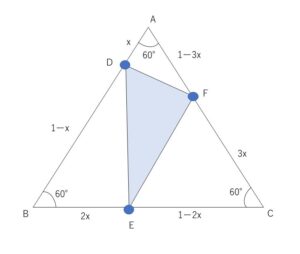
\(S=△DEF=△ABC\)\(-(△ADF+△DBE+△ECF)\) であり
\(△ABC=\displaystyle\frac{1}{2}・1・1・\sin60°=\displaystyle\frac{\sqrt{3}}{4}\)
\(△ADF+△DBE+△ECF\)
\(=\displaystyle\frac{1}{2}\{x(1-3x)+2x(1-x)+3x(1-2x)\}\sin60°\)
\(=\displaystyle\frac{\sqrt{3}}{4}x(6-11x)\)
よって
\(S=\displaystyle\frac{\sqrt{3}}{4}-\displaystyle\frac{\sqrt{3}}{4}x(6-11x)\)
\(=\)\(\displaystyle\frac{\sqrt{3}}{4}(11x^2-6x+1)\)
ただし、\(0<x<1,0<2x<1,0<3x<1\) だから
\(0<x<\displaystyle\frac{1}{3}\)
(2)
ただの2次関数の最小値を求める問題です。
\(S=\displaystyle\frac{\sqrt{3}}{4}(11x^2-6x+1)\)
\(=\displaystyle\frac{\sqrt{3}}{4}\{11(x-\displaystyle\frac{3}{11})^2+\displaystyle\frac{2}{11}\}\) (\(0<x<\displaystyle\frac{1}{3}\))
\(=\displaystyle\frac{\sqrt{3}}{4}\{11(x-\displaystyle\frac{3}{11})^2+\displaystyle\frac{2}{11}\}\) (\(0<x<\displaystyle\frac{1}{3}\))
\(x^2\)の係数は正で、\(0<\displaystyle\frac{3}{11}<\displaystyle\frac{1}{3}\) だから、最小値をとる\(x\)の値は \(x=\displaystyle\frac{3}{11}\)
このとき最小値は \(\displaystyle\frac{\sqrt{3}}{4}・\displaystyle\frac{2}{11}=\)\(\displaystyle\frac{\sqrt{3}}{22}\)
このとき最小値は \(\displaystyle\frac{\sqrt{3}}{4}・\displaystyle\frac{2}{11}=\)\(\displaystyle\frac{\sqrt{3}}{22}\)
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。
ここまで読んで下さりありがとうございました。