平行四辺形の頂点の座標に関する問題について見ていきます。
(例題)
4点 \(A(-1,1\)),\(B(1,-2)\),\(C(5,0)\),\(D(x,y)\) がある。
(1)4点を頂点とする平行四辺形\(ABCD\)の頂点\(D\)の座標を求めよ。
(2)4点を頂点とする四角形が平行四辺形となるような点\(D\)の座標を求めよ。
(1)は平行四辺形\(ABCD\)と記載があり、\(ABCD\)がこの順番で並んでいるので平行四辺形は1通りに決まります。
一方(2)は4点の順番が決まっていないので、複数の平行四辺形ができる可能性があります。
(解答)
(1)
\(D\)の求め方については
「平行四辺形 \(\leftrightarrow\) 対角線がそれぞれの中点で交わる」
を利用します。
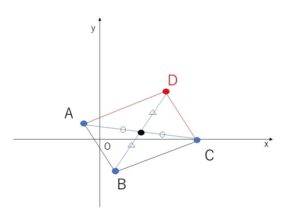
平行四辺形は図のようになり、対角線\(AC,BD\)の中点が一致するので
\(\displaystyle\frac{-1+5}{2}\)\(=\displaystyle\frac{1+x}{2}\), \(\displaystyle\frac{1+0}{2}\)\(=\displaystyle\frac{-2+y}{2}\)
よって \(x=3\), \(y=3\)
したがって \(D(3,3)\)
(2)
もちろん(1)の平行四辺形\(ABCD\)もこの3通りの中に含まれています。
図より平行四辺形は3通り考えられる。
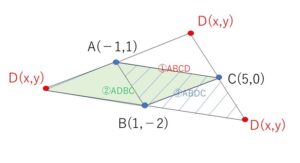
①平行四辺形\(ABCD\)の場合
(1)より \(D(3,3)\)
②平行四辺形\(ADBC\)の場合
対角線\(AB,DC\)の中点が一致するので
\(\displaystyle\frac{-1+1}{2}\)\(=\displaystyle\frac{x+5}{2}\), \(\displaystyle\frac{1-2}{2}\)\(=\displaystyle\frac{y+0}{2}\)
よって \(x=-5\),\(y=-1\) だから \(D(-5,-1)\)
③平行四辺形\(ABDC\)の場合
対角線\(AD,BC\)の中点が一致するので
\(\displaystyle\frac{-1+x}{2}\)\(=\displaystyle\frac{1+5}{2}\), \(\displaystyle\frac{1+y}{2}\)\(=\displaystyle\frac{-2+0}{2}\)
よって \(x=7\),\(y=-3\) だから \(D(7,-3)\)
以上より\(D\)の座標は
\((3,3)\), \((-5,-1)\), \((7,-3)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→座標を用いた証明(点の座標) back→三角形の形状と重心