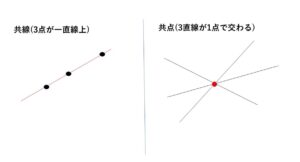
3点が同一直線上にある(共線)、3直線が1点で交わる(共点)に関する問題について見ていきます。
2点が異なれば、その2点を通る直線がただ1つに定まります。残り1点がその直線上にあれば3点が同一直線上にあることになります。
(共点について)
2直線が平行でなければ、2直線は1点で交わります。残り1本の直線がこの交点を通れば3直線が1点で交わることになります。
(例題1)
(1)3点 \(A(-2,3)\),\(B(1,2)\),\(C(3t+4,-2t+2)\) が同一直線上にあるとき、\(t\)の値を求めよ。
(2)3直線 \(x+y=3\), \(2x-y=0\), \(ax-2y=5\) が1点で交わるとき、定数\(a\)の値を求めよ。
(解答)
(1)
①ある直線 \(ax+by+c=0\) が、3点を通る
②\(AB\)を通る直線が\(C\)を通る
③\(AB\)の傾き\(=\)\(AC\)の傾き
などを考えます。解答では②の方法解いてみます。(③でも解けます)
\(A(-2,3)\),\(B(1,2)\) を通る直線は
\(y-3=\displaystyle\frac{2-3}{1+2}(x+2)\)
よって \(3y-9=-x-2\)・・・(A)
(A)上に\(C(3t+4,-2t+2)\) があるので
\(3(-2t+2)-9=-(3t+4)-2\)
ゆえに \(t=1\)
(2)
①3直線がある1点を通る
②2直線の交点を、残りの1直線が通る
③線分上の適当な分点が一致する
などを考えます。
(②の方法)
\(x+y=3\), \(2x-y=0\)の交点は、連立して解くことにより
\((1,2)\)
\(ax-2y=5\) が \((1,2)\)を通るので
\(a-4=5\)
よって \(a=9\)
(例題2)
3直線 \(x+2y=1\)・・・① \(3x-4y=1\)・・・② \(ax+by=1\)・・・③ について
(1)異なる3直線①②③が1点で交わるとき、3点\((1,2)\),\((3,-4)\),\((a,b)\)は同一直線上にあることを示せ。
(2)異なる3点\((1,2)\),\((3,-4)\),\((a,b)\)が同一直線上にあるとき、3直線①②③は1点で交わることを示せ。
(解答)
(1)
また、\((1,2)\),\((3,-4)\)を通る直線もすぐに求まります。
これらのことから\((a,b)\)が\((1,2)\),\((3,-4)\)を通る直線上にあることを示します。
①②の交点は連立して求めると
\((\displaystyle\frac{3}{5},\displaystyle\frac{1}{5})\)
③はこの交点を通るので \(\displaystyle\frac{3}{5}a+\displaystyle\frac{1}{5}b=1\)
両辺を\(5\)倍して \(3a+b=5\)・・・(A)
また\((1,2)\),\((3,-4)\)を通る直線は
\(y-2=\displaystyle\frac{-4-2}{3-1}(x-1)\) より
\(3x+y=5\)・・・(B)
(A)(B)より \((a,b)\)は \(3x+y=5\) 上にある。
よって3点は同一直線上にある。
(2)
(1)と同様に2点\((1,2)\),\((3,-4)\)を通る直線と、①②の交点を求めて、③が①②の交点を通ることを示します。
\((1,2)\),\((3,-4)\)を通る直線は(1)より
\(3x+y=5\)
この直線上に\((a,b)\)があるので \(3a+b=5\)・・・(C)
また①②の交点は(1)より \((\displaystyle\frac{3}{5},\displaystyle\frac{1}{5})\)
(C)の両辺を\(5\)で割って積の順序を入れ替えると・・・(※)
\(a・\displaystyle\frac{3}{5}+b・\displaystyle\frac{1}{5}=1\)
これは ③\(ax+by=1\) が \((\displaystyle\frac{3}{5},\displaystyle\frac{1}{5})\) を通ることを表している。
よって①②の交点を③が通ることになり、①②③は1点で交わる。
\(ap+bq=1\) という条件が与えられたときは、
(i)直線 \(ax+by=1\) が \((p,q)\)を通る
(ii)直線 \(px+qy=1\) が \((a,b)\)を通る
と2通りの見方ができることになります。このことを利用した(1)(2)の別解を紹介します。
(1の別解)
\(x+2y=1\)・・・① \(3x-4y=1\)・・・② \(ax+by=1\)・・・③ について
①②③は原点でない1点で交わり、その交点を\((p,q)\)(\(p≠0\)または \(q≠0\))とおくと
\(p+2q=1\), \(3p-4q=1\), \(ap+bq=1\)
積の順序を入れ替えて
\(p・1+q・2=1\), \(p・3+q・(-4)=1\), \(p・a+q・b=1\)・・・(ア)
\(px+qy=1\)は \(p≠0\)または \(q≠0\) より直線を表し
(ア)より 直線 \(px+qy=1\) は 3点\((1,2)\),\((3,-4)\),\((a,b)\) を通る。
よって3点は1直線上にある。
(2の別解)
3点\((1,2)\),\((3,-4)\),\((a,b)\)を通る直線を \(sx+ty=1\) (\(s≠0\)または \(t≠0\))とおくと
\(s+2t=1\)・・・(イ)
\(3s-4t=1\)・・・(ウ)
\(as+bt=1\)・・・(エ)
(イ)は \(x+2y=1\)・・・① が\((s,t)\)を通ることを示しており
同様に(ウ)(エ)は、\(3x-4y=1\)・・・② \(ax+by=1\)・・・③ が \((s,t)\)を通ることを示している。
したがって①②③は1点\((s,t)\)で交わる。
この解法は他の分野(例えば円と直線)でも応用がきくのでぜひマスターしましょう。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→共線・共点② back→折れ線の長さの最小値