座標を用いた三角形の面積を求める問題について見ていきます。
(例題)
3点 A\((-4,3)\),\(B(-1,2)\),\(C(3,-1)\) について、\(△ABC\)の面積を求めよ。
(解答)
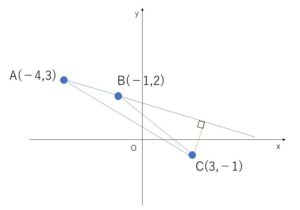
\(AB\)を底辺として考える。
\(AB=\sqrt{3^2+1^2}=\sqrt{10}\)
また、高さは直線\(AB\)と点\(C\)の距離\(h\)となる。
直線\(AB\)の方程式は \(y-2=-\displaystyle\frac{1}{3}(x+1)\) より
\(x+3y-5=0\)
よって
\(h=\displaystyle\frac{|3-3-5|}{\sqrt{1^2+3^2}}\) \(=\displaystyle\frac{5}{\sqrt{10}}\)
したがって
\(△ABC=\displaystyle\frac{1}{2}AB・h\)\(=\displaystyle\frac{1}{2}・\sqrt{10}・\displaystyle\frac{5}{\sqrt{10}}\)\(=\)\(\displaystyle\frac{5}{2}\)
座標を使った三角形の面積公式を利用した別解もあります。
こちらも重要なのでおさえておきましょう。
公式の導き方は今やった方法とほとんど同じです。
・三角形の面積公式(座標)
3点の座標が与えられた場合に、簡単にするため1点が原点にくるように平行移動すると、移動後の3点は \(O(0,0)\),\(A(x_1,y_1)\),\(B(x_2,y_2)\) とおけ、移動前の三角形の面積は\(△OAB\)の面積と同じです。よって\(△OAB\)について考えていきます。
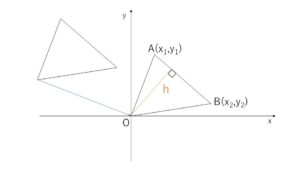
直線\(AB\)の方程式は \(x_1≠x_2\)のとき
\(y-y_1=\displaystyle\frac{y_2-y_1}{x_2-x_1}(x-x_1)\) より
\((y_2-y_1)(x-x_1)-(x_2-x_1)(y-y_1)=0\)・・・(※)
\(x_1=x_2\) のときは 直線\(AB\)の方程式は \(x=x_1\) となりますが、(※)に\(x_1=x_2\)を代入すると、\((y_2-y_1)(x-x_1)=0\)。3点は異なる点なので(同じだと三角形はできない)、\(y_2≠y_1\)より \(x-x_1=0\)。よって\(x_1=x_2\)のときも直線\(AB\)は(※)で表されます。
では、底辺を\(AB\)とすると\(△OAB\)の高さ\(h\)は、\(O(0,0)\)と直線\(AB\)の距離。(※)を整理すると
\((y_2-y_1)x-(x_2-x_1)y+x_2y_1-x_1y_2=0\)
よって
\(h=\displaystyle\frac{|x_2y_1-x_1y_2|}{\sqrt{(y_2-y_1)^2+(x_2-x_1)^2}}\)\(=\displaystyle\frac{|x_2y_1-x_1y_2|}{AB}\)
したがって
\(△OAB=\)\(\displaystyle\frac{1}{2}AB・h\)\(=\displaystyle\frac{1}{2}|x_2y_1-x_1y_2|\)\(=\)\(\displaystyle\frac{1}{2}|x_1y_2-x_2y_1|\)
\(S=\)\(\displaystyle\frac{1}{2}|x_1y_2-x_2y_1|\)
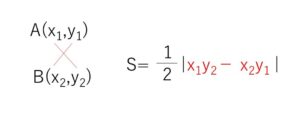
ではこの公式を利用して例題を解くと
3点 A\((-4,3)\),\(B(-1,2)\),\(C(3,-1)\) について \(C\)を原点にくるように、\(x\)軸方向に\(-3\),\(y\)軸方向に\(1\)だけ\(ABC\)を平行移動させると、
\(A→\)\(A'(-7,4)\), \(B→\)\(B'(-4,3)\), \(C→\)\(O(0,0)\) となるので
\(△ABC=△OA’B’\)\(=\displaystyle\frac{1}{2}|(-7)・3-4・(-4)|\)\(=\)\(\displaystyle\frac{5}{2}\)
と一瞬で求まります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→曲線と直線の距離 back→点と直線の距離