円と直線の位置関係について見ていきます。
・円と直線の位置関係
円と直線の位置関係は図示すると、次の3通りの場合に分類できます。
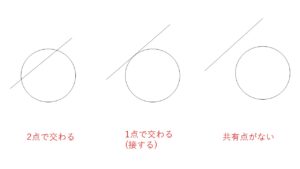
この位置関係を数式で考えてみましょう。
円: \((x-a)^2+(y-b)^2=r^2\)・・・① と 直線:\(y=mx+n\)・・・② について
①②を連立して解いたとき実数解\(x,y\)の組が存在すれば、①②はどちらも点\((x,y)\)を通るので、その解の組が共有点の座標となります。よって円と直線の連立方程式の実数解の組の個数が共有点の個数となります。
②を①に代入すると
\((x-a)^2+(mx+n-b)^2=r^2\)・・・③
②より\(x\)を1つ決めれば\(y\)は1つに決まるので、③の実数解の個数がそのまま共有点の個数となります。
また、③の\(x^2\)の係数は\(m^2+1\)であり、\(x\)の2次方程式なので、その判別式を\(D\)とすれば
\(D>0\) \(⇔\) 異なる2つの実数解をもつ=異なる2点で交わる
\(D=0\) \(⇔\) 実数解を1つもつ=1点で交わる(接する)
\(D<0\) \(⇔\) 実数解をもたない=共有点はない
と分類できます。
\((k-a)^2+(y-b)^2=r^2\) (\(y\)の2次方程式)
次に円と直線の位置関係を、円の中心と直線の距離と半径の大小に着目して考えてみます。
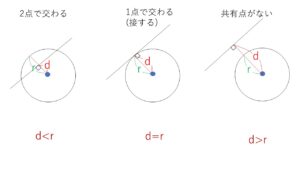
円の半径を\(r\)、直線と円の中心の距離を\(d\)とすれば図より
\(d<r\) \(⇔\) 異なる2点で交わる
\(d=r\) \(⇔\) 1点で交わる(接する)
\(d>r\) \(⇔\) 共有点がない
以上のことをまとめると次のようになります。
円と直線の位置関係について次のことが成り立つ。
・異なる2点で交わる \(⇔\) \(D>0\) \(⇔\) \(d<r\)
・1点で接する \(⇔\) \(D=0\) \(⇔\) \(d=r\)
・共有点をもたない \(⇔\) \(D<0\) \(⇔\) \(d>r\)
両方マスターしておきましょう。
(例題1)
円 \(x^2+y^2=5\) と 直線 \(2x-y+5=0\) は共有点をもつか。また、もつ場合にはその点の座標を求めよ。
(解答)
\(x^2+y^2=5\)・・・① \(2x-y+5=0\)・・・② について
②より \(y=2x+5\)・・・③
①に代入して
\(x^2+(2x+5)^2=5\)
\(5x^2+20x+20=0\)
\(x^2+4x+4=0\)
\((x+2)^2=0\) より
\(x=-2\)
③より \(y=1\)
よって共有点は1つで、円と直線は接する。
またその座標は \((-2,1)\)
(例題2)
座標平面上に、中心が\((2,2)\)で半径が\(1\)の円\(C\)と、原点を通り傾きが\(m\)の直線\(l\)がある。
(1)円\(C\)と直線\(l\)が異なる2点で交わるための\(m\)の値の範囲を求めよ。
(2)円\(C\)と直線\(l\)の2つの共有点と円\(C\)の中心とでできる三角形の面積が最大となるような\(m\)の値を求めよ。
(解答)
(1)円の中心と直線の距離\(d\)と半径\(1\)の大小について着目した解法
原点を通る傾き\(m\)の直線は \(y=mx\) より
\(-mx+y=0\)・・・①
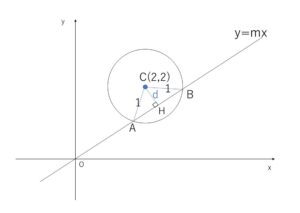
円と直線が2点で交わる条件は、円の中心\((2,2)\)と①の距離\(d\)を考えると、円の半径が\(1\)だから
\(d=\displaystyle\frac{|-2m+2|}{\sqrt{m^2+1}}<1\)
\(\sqrt{m^2+1}>0\)より
\(|-2m+2|<\sqrt{m^2+1}\)
両辺\(0\)以上の値なので2乗して
\((-2m+2)^2<m^2+1\)
整理すると
\(3m^2-8m+3<0\)
よって
\(\displaystyle\frac{4-\sqrt{7}}{3}<m<\displaystyle\frac{4+\sqrt{7}}{3}\)
(別解)判別式を利用する方法
直線\(l:y=mx\)・・・① 円\(C:(x-2)^2+(y-2)^2=1\)・・・② について
①を②に代入して
\((x-2)^2+(mx-2)^2=1\)
整理すると
\((m^2+1)x^2-2(2m+2)x+7=0\)
2点で交わるとき \(D>0\)より
\(\displaystyle\frac{D}{4}=(2m+2)^2-7(m^2+1)\)\(>0\)
整理すると
\(3m^2-8m+3<0\) だから
\(\displaystyle\frac{4-\sqrt{7}}{3}<m<\displaystyle\frac{4+\sqrt{7}}{3}\)
(2)
(1)より円と直線の距離\(d\)は \(\displaystyle\frac{|-2m+2|}{\sqrt{m^2+1}}\) であり
これは底辺を\(AB\)としたときの\(△ABC\)の高さとなるので、\(AB\)の長さを求めて、\(△ABC\)の面積を\(m\)で表して・・・とやると複雑な式となり大変そうです。
そこで面積が最大となるときの三角形の形状について考えてみます。
\(△ABC\)は \(CA=CB=1\) の二等辺三角形であり特徴的な三角形です。\(CA=CB\)の挟む角を \(\angle ACB=θ\) とおくと、面積は \(\displaystyle\frac{1}{2}・1^2・\sinθ\) だから、\(θ=90°\)のとき最大となることが分かります。(このとき\(△ABC\)は直角二等辺三角形となる)
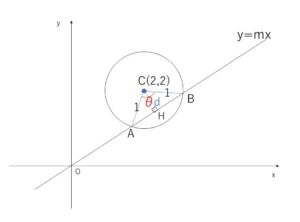
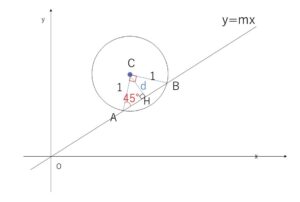
直線\(l\)と円の交点を\(A,B\)、円の中心を\(C\)、\(C\)から\(l\)に下した垂線の足を\(H\)とする。
\(\angle ACB=θ\) とおくと、\(0°<θ<180°\) であり、三角形の面積\(S\)は
\(S=\displaystyle\frac{1}{2}・1^2・\sinθ=\displaystyle\frac{1}{2}\sinθ\)
よって、\(θ=90°\)のとき \(S\)は最大となる。
このとき、\(△ABC\)は\(CA=CB\)の直角二等辺三角形だから、\(\angle CAB=45°\)
\(△CAH\)も直角三角形であるから、\(d=CH=1・\sin45°\)\(=\displaystyle\frac{1}{\sqrt{2}}\)
ゆえに(1)より
\(d=\displaystyle\frac{|-2m+2|}{\sqrt{m^2+1}}=\displaystyle\frac{1}{\sqrt{2}}\)・・・(A)
(A)より
\(\sqrt{2}|-2m+2|=\sqrt{m^2+1}\)
両辺\(0\)以上の値なので2乗して整理すると
\(7m^2-16m+7=0\)
したがって \(m=\displaystyle\frac{8±\sqrt{15}}{7}\)
としたので、\(m=\displaystyle\frac{8±\sqrt{15}}{7}\) はもちろん(1)で求めた範囲内にあります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の接線の方程式① back→2次の方程式の表す図形