円の接線の方程式③

円の接線の方程式に関する発展的な問題について見ていきます。

(例題)
\(xy\)平面上の円周 \(x^2+y^2=1\) 上の接線\(l\)に、定点\(P(p,0)\),\(Q(-q,0)\) \((1<q<p)\) から引いた垂線の足をそれぞれ\(R,S\)とする。
(1)\(PR^2+QS^2\)の最小値を求めよ。
(2)\(PR+QS\)を最小にする接線\(l\)を求めよ。

(解答)
(1)

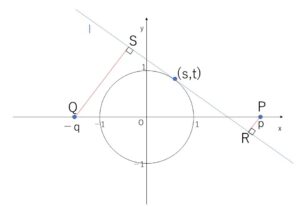
接点を\((s,t)\)とおくと、円上の点なので
\(s^2+t^2=1\), 　(\(-1≦s≦1\))

また接線の方程式は \(sx+ty=1\)　(\(sx+ty-1=0\)) より

\(PR=\displaystyle\frac{|sp-1|}{\sqrt{s^2+t^2}}\)\(=|sp-1|\)
\(QS=\displaystyle\frac{|-sq-1|}{\sqrt{s^2+t^2}}\)\(=|sq+1|\)

よって
\(PR^2+QS^2\)
\(=(sp-1)^2+(sq+1)^2\)

\(=(p^2+q^2)s^2-2(p-q)s+2\)　(\(s\)の2次関数なので平方完成します)
\(=(p^2+q^2)(s^2-\displaystyle\frac{2(p-q)}{p^2+q^2}s)+2\)
\(=(p^2+q^2)(s-\displaystyle\frac{p-q}{p^2+q^2})^2\)\(-\displaystyle\frac{(p-q)^2}{p^2+q^2}\)\(+2\)
\(=(p^2+q^2)(s-\displaystyle\frac{p-q}{p^2+q^2})^2\)\(+\displaystyle\frac{p^2+2pq+q^2}{p^2+q^2}\)
(ただし \(-1≦s≦1\))

ここで、\(p>q\)より
\(\displaystyle\frac{p-q}{p^2+q^2}>0\)
また
\(p^2+q^2-(p-q)\)
\(=p(p-1)+q^2+q\)\(>0\)　(\(p>1,q>1\) より)
よって \(p^2+q^2>p-q\) であり、\(p^2+q^2>0\)より
\(\displaystyle\frac{p-q}{p^2+q^2}<1\)

ゆえに 軸が\(-1≦s≦1\)の範囲内にあるので
最小値は \(\displaystyle\frac{p^2+2pq+q^2}{p^2+q^2}\)

(2)
(1)より
\(PR+QS=|ps-1|+|qs+1|\)　(\(-1≦s≦1\))

今度は絶対値を含む\(s\)の1次関数です。(\(p,q\)は定数)
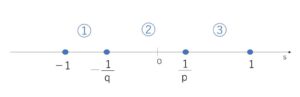
境目は \(\displaystyle\frac{1}{p}\)と \(-\displaystyle\frac{1}{q}\) で、\(-1<-\displaystyle\frac{1}{q}\)\(<\displaystyle\frac{1}{p}\)\(<1\)　なので
①\(-1≦s≦-\displaystyle\frac{1}{q}\)　②\(-\displaystyle\frac{1}{q}≦s≦\displaystyle\frac{1}{p}\) ③\(\displaystyle\frac{1}{p}≦s≦1\)
で場合分けします。

①\(-1≦s≦-\displaystyle\frac{1}{q}\) のとき
\(ps-1<0\),　\(qs+1≦0\) より
\(PR+QS\)\(=-(ps-1)-(qs+1)\)\(=-(p+q)s\)
傾き\(-(p+q)\)は負の値なので、常に減少(右下がりのグラフ)

②\(-\displaystyle\frac{1}{q}≦s≦\displaystyle\frac{1}{p}\) のとき
\(ps-1≦0\),　\(qs+1≧0\) より
\(PR+QS\)\(=-(ps-1)+(qs+1)\)\(=-(p-q)s+2\)
傾き\(-(p-q)s+2\)は負の値なので、常に減少(右下がりのグラフ)

③\(\displaystyle\frac{1}{p}≦s≦1\)のとき
\(ps-1≧0\), \(qs+1>0\) より
\(PR+QS\)\(=(ps-1)+(qs+1)\)\(=(p+q)s\)
傾き\(p+q\)は正の値なので、常に増加(右上がりのグラフ)

①～③より\(PR+QS\)のグラフは次のようになる。

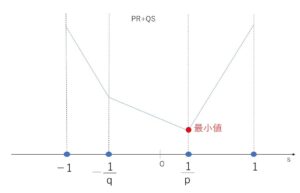
ゆえに 最小値をとるとき \(s=\displaystyle\frac{1}{p}\)

このとき \(s^2+t^2=1\) より
\(t=±\sqrt{1-\displaystyle\frac{1}{p^2}}\)

したがって接線の方程式は
\(\displaystyle\frac{1}{p}x±\sqrt{1-\displaystyle\frac{1}{p^2}}y=1\)

出てきた2本の接線(\(x\)軸対称)は両方答えとなります。なぜなら対称性から一方の接点\((s,t)\)の接線に対して、\(x\)軸対称な点\((s,-t)\)における接線も条件が同じになるからです。
ちなみに\(\displaystyle\frac{1}{p}x±\sqrt{1-\displaystyle\frac{1}{p^2}}y=1\) を図示すると次の通りです。この接線は\(P(p,0)\)を通ります。

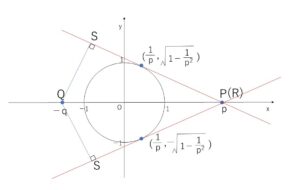
少し難しかったでしょうか。じっくり考えて理解しましょう。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の2接点を通る直線(極線)　back→円の接線の方程式②