正領域・負領域に関する問題について見ていきます。
まずは正領域・負領域についておさらいしていきましょう。
・正領域・負領域
\(x,y\)についての不等式\(f(x,y)\)について、\(f(x,y)>0\)の表す領域を\(f(x,y)\)の正領域、\(f(x,y)<0\)の表す領域を\(f(x,y)\)の負領域といいます。
(例)
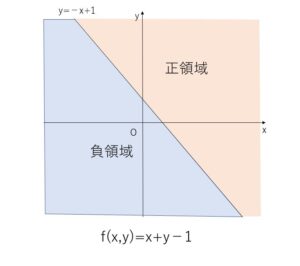
\(f(x,y)=x+y-1\) について
正領域は \(f(x,y)=x+y-1>0\) つまり \(y>-x+1\)
負領域は \(f(x,y)=x+y-1<0\) つまり \(y<-x+1\)
境界線は \(x+y-1=0\)、つまり \(f(x,y)=0\) (右辺が\(0\)の形の式)となる。
(例題1)
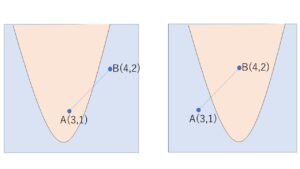
曲線 \(y=x^2-2x+a\) に関して、点\(A(3,1)\)と点\(B(4,2)\)が互いに反対側にあるとき、\(a\)の値の範囲を求めよ。
①は \(y-x^2+2x-a=0\) と変形できるので(\(=0\)の形にする)、
\(f(x,y)=y-x^2+2x-a\) とおくと、2点の座標をこの式に代入したときに、一方が正、一方が負になります(1点が正領域、もう1点が負領域にある)。
組合せとしては、(1)点A正,点B負 (2)点A負,点B正 の2パターンですが、これをまとめて、\(f(3,1)×f(4,2)<0\) とすると楽です。
(解答)
\(f(x,y)=y-x^2+2x-a\) とおくと、求める条件は
\(f(3,1)×f(4,2)<0\)
よって
\((1-9+6-a)(2-16+8-a)<0\)
\((-a-2)(-a-6)<0\)
\(-(a+2)・(-1)(a+6)<0\)
\((a+2)(a+6)<0\)
したがって \(-6<a<-2\)
(例題2)
\(xy\)平面上の原点と点\((1,2)\)を結ぶ線分(両端を含む)を\(L\)とする。
曲線 \(y=x^2+ax+b\) が\(L\)と共有点をもつような実数の組\((a,b)\)の集合を\(ab\)平面に図示せよ。
\(f(0,0)・f(1,2)≦0\) (端点が曲線上にあるときも含めて\(=\)をつけた)
と考えることができますが、もちろんこの条件以外にも、線分\(L\)と曲線が2点で交わる場合や、端点以外で接する場合なども考えなくてはなりません。
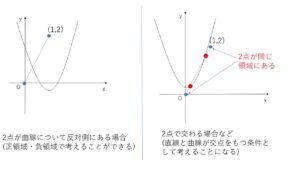
結局2点で交わる場合などについては、\(L\)を延長した直線と曲線が \(0≦x≦1\) で解をもつ条件を考えることなるので、最初からすべての場合について直線と曲線を連立した2次方程式の解の条件問題として解答していきたいと思います。
(解答)
原点と点\((1,2)\)を結ぶ直線の方程式は、\(y=2x\)
これと 曲線 \(y=x^2+ax+b\) より\(y\)を消去して
\(2x=x^2+ax+b\)
\(x^2+(a-2)x+b=0\)・・・①
求める\(a,b\)の条件は、\(x\)の2次方程式①が\(0≦x≦1\) の範囲で少なくとも1つの実数解をもつ条件となる。
(1)\(0≦x≦1\)の範囲に2つの実数解をもつ (重解を含む)
(2)\(0<x<1\)の範囲にただ1つの実数解をもつ または \(x=0\) or \(x=1\)を解にもつ
に場合分けできます。重解は解としての\(x\)は1つですが、\(0≦x≦1\) のすべての\(x\)で可能性があるため(1)に混ぜ込みます。
(1)は判別式、軸、端点の3つに着目して、(2)は\(g(x)=x^2+(a-2)x+b\) とおくと、\(g(0)・g(1)<0\) または \(g(0)・g(1)=0\) となるのでまとめて
\(g(0)・g(1)≦0\) とします。
\(g(x)=x^2+(a-2)x+b\) おくと、\(y=g(x)\)は下に凸のグラフ。
(1)\(0≦x≦1\)の範囲に2つの実数解をもつ (重解を含む) とき
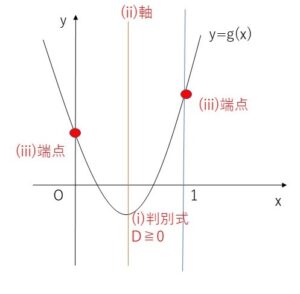
(i)判別式\(D≧0\)
(ii)軸 \(0≦-\displaystyle\frac{a-2}{2}≦1\)
(iii)端点 \(g(0)≧0\) かつ \(g(1)≧0\)
(i)は \(D=(a-2)^2-4b≧0\)
つまり、\(b≦\displaystyle\frac{1}{4}(a-2)^2\)
(ii)は \(0≦-a+2≦2\)
つまり、\(0≦a≦2\)
(iii)は \(b≧0\) かつ \(1+a-2+b≧0\)
つまり、\(b≧0\) かつ \(b≧-a+1\)
(2)\(0<x<1\)の範囲にただ1つの実数解をもつ または \(x=0\) or \(x=1\)を解にもつとき
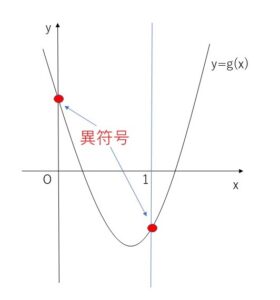
\(g(0)・g(1)≦0\) より
\(b(1+a-2+b)≦0\)
\(b(a+b-1)≦0\)
よって
\(b≧0\) かつ \(a+b-1≦0\) (\(b≦-a+1\))
または
\(b≦0\) かつ \(a+b-1≧0\) (\(b≧-a+1\))
以上から(1)(2)を合わせたものを\(ab\)平面に図示すると次の通り。
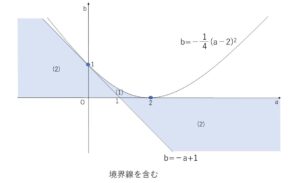
別にして考えると
(ア)\(0<x<1\) で2つの実数解をもつ(重解を含む)
(イ)\(0<x<1\) でただ1つの実数解をもつ
(ウ)\(x=0\) または \(x=1\) を解にもつ
となります。この場合分けは、数IA →(8-7)ある区間に少なくとも1つの解 と同じ方法です。こちらも参考にしてみてください。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→領域と最大・最小値①(基礎) back→不等式の表す領域③(積の形)