三角関数の周期性と公式

三角関数の\(θ+α\)の公式について見ていきます。

以下単位円で考えていきます。
(\(\sinθ=y\), \(\cosθ=x\), \(\tanθ=\)\(\displaystyle\frac{y}{x}\))

①\(θ+2nπ\) (\(n\)は整数)の公式
角\(θ\)の動径は、反時計回り(時計回り)に1,2,3・・・周すると、もとの位置に戻る。よって\(θ\)のときと三角関数の値は変わらないので

②\(-θ\)の公式

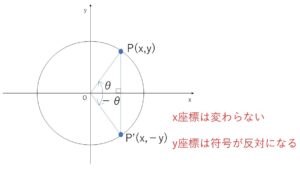
まず\(θ\)を\(0°≦θ≦90°\) の範囲で考えます。
角\(-θ\)の動径\(OP’\)は、角\(θ\)の動径\(OP\)と\(x\)軸について対称な位置にあります。よって点\(P(x,y)\)とおくと、点\(P'(x,-y)\)\(=(\cos(-θ),\sin(-θ))\) であるから

\(\cos(-θ)=x=\cosθ\)・・・(1)
\(\sin(-θ)=-y=-\sinθ\)・・・(2)
\(\tan(-θ)=\displaystyle\frac{-y}{x}\)\(=-\tanθ\)・・・(3)

また、\(90°≦θ<360°\) (第2～4象限と軸の部分) でも同様のことが成り立ち、
さらに\(0≦θ<360°\) の範囲にない場合でも、公式①より\(2nπ\)を加えることで\(0≦θ<360°\)の場合に帰着できます。

以上より一般角\(θ\)について(1)～(3)が成り立ちます。

(注)以下③以降の公式についても、\(0≦θ<360°\)について考えるべきですが量が多くなってしまうので\(0≦θ≦90°\)のみについて考えていきます(\(90°≦θ<360°\)でも成り立ちます)。最初はちゃんと成り立つかどうか確認したほうがよいですが、実際に試験で使うときは \(0≦θ≦90°\)についてだけ考えて公式を導けばよいです。

③\(θ+π\),\(θ+\displaystyle\frac{π}{2}\) の公式

・\(θ+π\)について

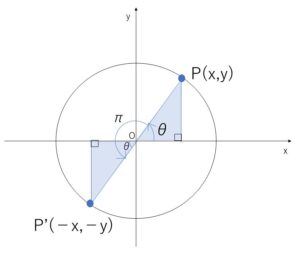
角\(θ\)の動径\(OP\)を\(π\)だけ回転すると、角\(θ+π\)の動径\(OP’\)になります。この2つの動径は原点について対称な位置にあるので、\(P(x,y)\)とすれば、\(P'(-x,-y)\)\(=(\cos(θ+π),\sin(θ+π))\)

よって
\(\cos(θ+π)=-x=-\cosθ\)
\(\sin(θ+π)=-y=-\sinθ\)
\(\tan(θ+π)=\displaystyle\frac{-y}{-x}=\)\(\displaystyle\frac{y}{x}\)\(=\tanθ\)

・\(θ+\displaystyle\frac{π}{2}\)について

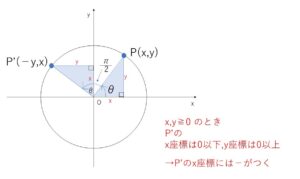
角\(θ\)の動径\(OP\)を\(\displaystyle\frac{π}{2}\)だけ回転すると、角\(θ+\displaystyle\frac{π}{2}\)の動径\(OP’\)になります。2つの合同な直角三角形に着目して、\(x,y≧0\)　(\(0°≦θ≦90°\))　で、\(P’\)の\(x\)座標は\(0\)以下,\(y\)座標は\(0\)以上だから、\(P’\)の座標は\((-y,x)=(\cos(θ+\displaystyle\frac{π}{2}),\sin(θ+\displaystyle\frac{π}{2}))\)

よって
\(\cos(θ+\displaystyle\frac{π}{2})=-y=-\sinθ\)
\(\sin(θ+\displaystyle\frac{π}{2})=x=\cosθ\)
\(\tan(θ+\displaystyle\frac{π}{2})=\displaystyle\frac{x}{-y}\)\(=-\displaystyle\frac{1}{\tanθ}\)

④\(π-θ\),\(\displaystyle\frac{π}{2}-θ\) の公式

・\(π-θ\)について

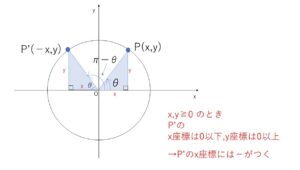
図のように\(P(x,y)\)と\(P’\)をとる。2つの合同な直角三角形に着目して、\(x,y≧0\) のとき、\(P’\)の\(x\)座標は\(0\)以下、\(y\)座標は\(0\)以上だから、
\(P'(-x,y)=(\cos(π-θ),\sin(π-θ))\)

よって
\(\cos(π-θ)=-x\)\(=-\cosθ\)
\(\sin(π-θ)=y\)\(=\sinθ\)
\(\tan(π-θ)=\displaystyle\frac{y}{-x}\)\(=-\tanθ\)

・\(\displaystyle\frac{π}{2}-θ\) について

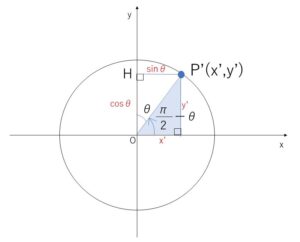
図のように\(P'(x’,y’)\)\(=(\cos(\displaystyle\frac{π}{2}-θ),\sin(\displaystyle\frac{π}{2}-θ))\)と、\(P’\)から\(y\)軸に下した垂線の足\(H\)をとる。
\(0°≦θ≦90°\)において、\(\sinθ≧0\),\(\cosθ≧0\)で、\(x’,y’≧0\) だから
\(P’H=\sinθ=x’\),　\(OH=\cosθ=y’\)

よって
\(\cos(\displaystyle\frac{π}{2}-θ)=x’\)\(=\sinθ\)
\(\sin(\displaystyle\frac{π}{2}-θ)=y’\)\(=\cosθ\)
\(\tan(\displaystyle\frac{π}{2}-θ)=\displaystyle\frac{y’}{x’}\)\(=\displaystyle\frac{\cosθ}{\sinθ}\)\(=\displaystyle\frac{1}{\tanθ}\)

(補足1)\(\tanθ\)の公式ついては、定義されない角の場合は除きます

(補足2)\(π-θ\)と\(\displaystyle\frac{π}{2}±θ\) については、角の制限はありましたが三角比(数ⅠA)のところで成り立った式と同じです。角の制限があったのは、数ⅠAでは三角比の角を0°以上180°以下の範囲で定義していたからです。
よって一般角でも成り立つ今回の公式のほうでまとめて理解しておけばよいです。

(例題1)次の式の値を求めよ。
\(\sin1020°\)+\(\cos(-240°)\)+\(\tan(-1020°)\)

(解答)
\(\sin1020°=\sin(300°+360°×2)\)\(=\sin300°\)
\(\sin300°=\sin(180°+120°)\)\(=-\sin120°\)\(=-\sin(180°-60°)\)\(=-\sin60°\)\(=-\displaystyle\frac{\sqrt{3}}{2}\)

\(\cos(-240°)\)\(=\cos240°\)\(=\cos(180+60°)\)\(=-\cos60°\)\(=-\displaystyle\frac{1}{2}\)

\(\tan(-1020°)=\tan(60°+360°×(-3))\)\(=\tan60°\)\(=\sqrt{3}\)

したがって
(与式)
\(=-\displaystyle\frac{\sqrt{3}}{2}-\displaystyle\frac{1}{2}+\sqrt{3}\)
\(=\)\(-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}\)

(例題2)
(1)\(\sin(θ+\displaystyle\frac{3}{2}π)\), \(\cos(θ+\displaystyle\frac{3}{2}π)\), \(\tan(θ+\displaystyle\frac{3}{2}π)\) それぞれを、\(\sinθ\),\(\cosθ\),\(\tanθ\)のどれか1つを使って表せ。
(2)\(\sin(\displaystyle\frac{3}{2}π-θ)\), \(\cos(\displaystyle\frac{3}{2}π-θ)\), \(\tan(\displaystyle\frac{3}{2}π-θ)\) それぞれを、\(\sinθ\),\(\cosθ\),\(\tanθ\)のどれか1つを使って表せ。

(解答)
(1)
\(\sin(θ+\displaystyle\frac{3}{2}π)\)\(=\sin\{(θ+\displaystyle\frac{π}{2})+π\}\)\(=-\sin(θ+\displaystyle\frac{π}{2})\)\(=-\cosθ\)
\(\cos(θ+\displaystyle\frac{3}{2}π)\)\(=\cos\{(θ+\displaystyle\frac{π}{2})+π\}\)\(=-\cos(θ+\displaystyle\frac{π}{2})\)\(=\sinθ\)
\(\tan(θ+\displaystyle\frac{3}{2}π)\)\(=\displaystyle\frac{\sin(θ+\displaystyle\frac{3}{2}π)}{\cos(θ+\displaystyle\frac{3}{2}π)}\)\(=\displaystyle\frac{-\cosθ}{\sinθ}\)\(=-\displaystyle\frac{1}{\tanθ}\)

(2)
\(\sin(\displaystyle\frac{3}{2}π-θ)\)\(=\sin\{π-(θ-\displaystyle\frac{π}{2})\}\)\(=\sin(θ-\displaystyle\frac{π}{2})\)\(=-\sin(\displaystyle\frac{π}{2}-θ)\)\(=-\cosθ\)
\(\cos(\displaystyle\frac{3}{2}π-θ)\)\(=\cos\{π-(θ-\displaystyle\frac{π}{2})\}\)\(=-\cos(θ-\displaystyle\frac{π}{2})\)\(=-\cos(\displaystyle\frac{π}{2}-θ)\)\(=-\sinθ\)
\(\tan(\displaystyle\frac{3}{2}π-θ)\)\(=\displaystyle\frac{\sin(\displaystyle\frac{3}{2}π-θ)}{\cos(\displaystyle\frac{3}{2}π-θ)}\)\(=\displaystyle\frac{-\cosθ}{-\sinθ}\)\(=\displaystyle\frac{1}{\tanθ}\)

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→三角関数のグラフ①　back→解が三角関数となる2次方程式