順列の知識を用いて、特定の条件がついた人の並べ方について考えてみます。
(問題)
男子\(A,B,C,D\)と女子\(E,F,G\)の7人が1列に並ぶとき
(1)並び方の総数は何通りあるか。
(2)男子が両端にくる並び方は何通りあるか。
(3)女子\(E,F\)が隣り合う並び方は何通りあるか。
(4)どの女子も隣り合わない並び方は何通りあるか。
(解答)
(1)
7人が1列に並ぶ順列より
\(7!=7・6・5・4・3・2・1=\)\(5040\)(通り)
(2)
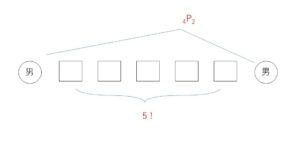
男子4人のうち、男子を合計2人両端に並べるので、\({}_4\mathrm{P}_2\)\(=4・3=12\)(通り)
残りの男子2人と女子3人を内側に並べる方法は、\(5!=5・4・3・2・1=120\)(通り)
よって、求める並び方は \(12×120=\)\(1440\) (通り)
(3)
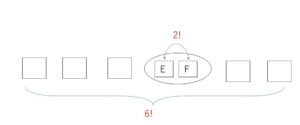
\(E,F\)が隣り合うので、\(E,F\)をひとかたまりとします。例えば手をつないでしまうと考えると分かりやすいでしょう。
そうすると残りの5人と\(E,F\)のひとかたまりの計6個の順列となります。ただし\(E,F\)の中でも順番があることを忘れないように。\(EF,FE\)の合計\(2!\)通りの順列があります。
そうすると残りの5人と\(E,F\)のひとかたまりの計6個の順列となります。ただし\(E,F\)の中でも順番があることを忘れないように。\(EF,FE\)の合計\(2!\)通りの順列があります。
\(E,F\)1組と残り5人の並び方は、\(6!\)(通り)
\(E,F\)の並び方は、\(2!\)(通り)
よって、求める並び方は \(6!×2!=720×2=\)\(1440\)(通り)
\(E,F\)の並び方は、\(2!\)(通り)
よって、求める並び方は \(6!×2!=720×2=\)\(1440\)(通り)

(4)
隣り合わない並べ方は、後から隙間に入れるという考え方を使います。
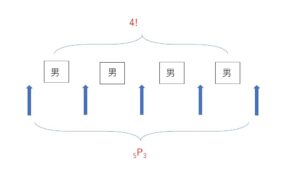
まず男子4人を1列に並べます。つぎのこの男子の間か両端の合計5か所のうち3か所に女子を入れて並べます。こうすると女子が隣り合わない場合を、もれなく重複なく数え上げることができます。
まず男子4人を1列に並べます。つぎのこの男子の間か両端の合計5か所のうち3か所に女子を入れて並べます。こうすると女子が隣り合わない場合を、もれなく重複なく数え上げることができます。
男子4人の並び方は、\(4!\)(通り)
この男子の間と両端の合計5か所のうち3か所に女子\(E,F,G\)を並べればよいので、その並べ方は \({}_5\mathrm{P}_3\)(通り)
よって、求める並べ方は
\(4!×{}_5\mathrm{P}_3=\)\(24×60=\)\(1440\)(通り)
この男子の間と両端の合計5か所のうち3か所に女子\(E,F,G\)を並べればよいので、その並べ方は \({}_5\mathrm{P}_3\)(通り)
よって、求める並べ方は
\(4!×{}_5\mathrm{P}_3=\)\(24×60=\)\(1440\)(通り)
\({}_5\mathrm{P}_3\)は次のように考えると分かりやすいでしょう。
女子\(E\)の並ぶ場所の選び方は、5通り
女子\(F\)の並ぶ場所の選び方は、\(E\)が選んだ以外の 4通り
女子\(G\)の並ぶ場所の選び方は、\(E,F\)が選んだ以外の 3通り
よって並び方の総数は \({}_5\mathrm{P}_3\)
女子\(E\)の並ぶ場所の選び方は、5通り
女子\(F\)の並ぶ場所の選び方は、\(E\)が選んだ以外の 4通り
女子\(G\)の並ぶ場所の選び方は、\(E,F\)が選んだ以外の 3通り
よって並び方の総数は \({}_5\mathrm{P}_3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。