共通接線①(2曲線が接する)

これから共通接線に関する問題について扱っていきますが、この辺りで、整式で表される関数について「接する \(⇔\) 重解を持つ」を示しておきます。

・接する2曲線
2曲線 \(y=f(x)\) と \(y=g(x)\) が、共有点をもち、その共有点における接線が一致するとき、「2曲線が接する」といい、この共有点を接点とよびます。

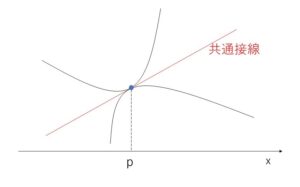
2曲線の交点(接点)の\(x\)座標を\(p\)とすると、2曲線の接線はそれぞれ

\(y=f'(p)(x-p)+f(p)\)
\(y=g'(p)(x-p)+g(p)\)

となるので、傾きと切片を比べると

\(f'(p)=g'(p)\)
\(-f'(p)p+f(p)=-g'(p)p+g(p)\)

つまり
\(f'(p)=g'(p)\)
\(f(p)=g(p)\)

が2曲線が接する条件となります。

・重解と接する
整式で表される2つの関数 \(y=f(x)\) と \(y=g(x)\) において、\(y\)を消去した\(x\)の方程式

\(f(x)-g(x)=0\)

について、次のことが成り立ちます。

(証明) (積の微分を使います)

\(→\) について
\(f(x)-g(x)=(x-a)^2h(x)\)・・・① とおける。

①に \(x=a\) を代入すると
\(f(a)-g(a)=0\)
\(f(a)=g(a)\)・・・②

①の両辺を\(x\)で微分すると
\(f'(x)-g'(x)=2(x-a)h(x)+(x-a)^2h'(x)\)
\(x=a\) を代入して
\(f'(a)-g'(a)=0\)
\(f'(a)=g'(a)\)・・・③

②③より \((a,f(a))\) \(\{=(a,g(a))\}\)で接している。

\(←\) について
\((a,f(a))\)で接しているので
\(f'(a)=g'(a)\)・・・④
\(f(a)=g(a)\)・・・⑤

⑤と因数定理から
\(f(x)-g(x)=(x-a)H(x)\)・・・⑥

両辺\(x\)で微分すると
\(f'(x)-g'(x)=H(x)+(x-a)H'(x)\)
\(x=a\)を代入して
\(f'(a)-g'(a)=H(a)\)
④より
\(H(a)=0\) だから
\(H(x)\) も因数 \(x-a\) をもち
\(H(x)=(x-a)I(x)\)・・・⑦

⑥⑦から
\(f(x)-g(x)=(x-a)^2I(x)\)　(重解をもつ)

(例題1)
次の両曲線が接するときの\(a\)の値を求めよ。
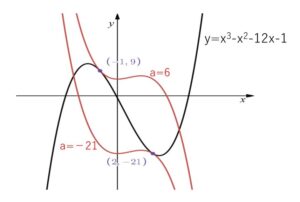
\(y=x^3-x^2-12x-1\)
\(y=-x^3+2x^2+a\)

(解答1)微分係数を利用する解法
それぞれ微分すると
\(y’=3x^2-2x-12\)
\(y’=-3x^2+4x\)

交点の\(x\)座標を\(p\)とおくと、2曲線が接する条件は

\(p^3-p^2-12p-1=-p^3+2p^2+a\)・・・①
\(3p^2-2p-12=-3p^2+4p\)・・・②

②より
\(p^2-p-2=0\)
\((p+1)(p-2)=0\)
\(p=-1,2\)

①より
\(a=2p^3-3p^2-12p-1\)
\(p=-1,2\) を代入して
\(a=6,-21\)

(解法2)重解を利用する方法
\(y=x^3-x^2-12x-1\)
\(y=-x^3+2x^2+a\)

\(y\)を消去して
\(x^3-x^2-12x-1=-x^3+2x^2+a\)
\(2x^3-3x^2-12x-a-1=0\)・・・③

接点の\(x\)座標を\(p\)、③のもう1つの解を\(q\)とすれば

\(2x^3-3x^2-12x-a-1=2(x-p)^2(x-q)\)  (\(q\)は実数)

と表せる。右辺を展開すると
\(2(x-p)^2(x-q)\)
\(=2x^3-(4p+2q)x^2+(2p^2+4pq)x-2p^2q\)

よって係数比較して
\(4p+2q=3\)・・・④
\(2p^2+4pq=-12\)・・・⑤
\(-2p^2q=-a-1\)・・・⑥

④⑤より、\(p,q\) を求めると(詳細略)
\((p,q)=(-1,\displaystyle\frac{7}{2}),(2,-\displaystyle\frac{5}{2})\)

⑥より\(a\)の値はそれぞれ
\(a=6,-21\)

(例題2)
2曲線
\(y=x-x^3\)
\(y=x^3+px^2+qx+r\)
は、点\(P(-1,0)\) で共通の接線をもち、その接線上の、\(P\)以外の点で交わるような、\(p,q,r\) の値を求めよ。

2曲線が\(P\)で接していて、2曲線の他の交点が接線上にあるということです。
今回も微分係数と重解を使った2解法を紹介します。

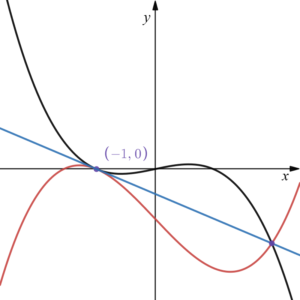
\(y=x-x^3\) と \(P(-1,0)\) より、接線は具体的に確定して、もう1つの交点も具体的に求まります。

(解法1)
\(f(x)=x-x^3\)
\(g(x)=x^3+px^2+qx+r\)
とおく。

\(f'(x)=1-3x^2\)
\(g'(x)=3x^2+2px+q\)

2曲線が、\((-1,0)\)で接するので
\(f(-1)=g(-1)\)
\(f'(-1)=g'(-1)\)

\(0=-1+p-q+r\)・・・①
\(-2=3-2p+q\)・・・②

ここで、\(f(x)=x-x^3\) の \((-1,0)\)における接線は(\(g(x)\)の接線でもある)

\(y=-2(x+1)\)

であるから、\(y=x-x^3\) と連立することにより\(P\)以外の交点を求めると
\(x-x^3=-2(x+1)\)
\(x^3-3x-2=0\)
\((x+1)^2(x-2)=0\)

したがって\(P\)以外の交点は
\((2,f(2))=(2,-6)\)

\(y=g(x)\) も \((2,-6)\) を通るから
\(-6=8+4p+2q+r\)・・・③

①②③より、\(p,q,r\)を求めて(詳細略)
\(p=0\), \(q=-5\), \(r=-4\)

(解法2)
(解法1)と同様に、接線と他の交点を求めると

接線: \(y=-2(x+1)\)
交点: \((2,-6)\)

\(y=x^3+px^2+qx+r\)
\(y=-2(x+1)\)

より\(y\)を消去すると
\(x^3+px^2+qx+r-\{-2(x+1)\}=0\)

この方程式は、\(x=-1\) を重解にもち、\(x=2\) を解にもつので

\(x^3+px^2+qx+r-\{-2(x+1)\}\)\(=(x+1)^2(x-2)\)

よって
\(x^3+px^2+qx+r\)\(=(x+1)^2(x-2)-2(x+1)\)

右辺を展開すると
\(x^3-5x-4\)
となるので係数比較して

\(p=0\), \(q=-5\), \(r=-4\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→共通接線②(異なる点で接する)　back→接線の基礎②