二重接線について見ていきます。
二重接線は、共通接線(接点が異なる場合)の2曲線が同じ曲線になっているだけなので、問題の解法は共通接線のときと同じで、整式の場合には「接する=重解」とすると早いです。
例題に入る前に軽く二重接線について触れておきます。
・二重接線
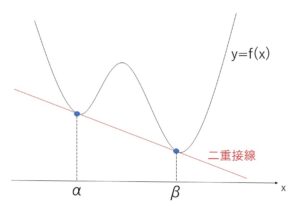
関数 \(y=f(x)\) に異なる2点で接する直線が存在するとき、この接線を二重接線とよびます。(同様に異なる3点,・・・で接する直線を三重接線,・・・という)
\(f(x)\) が整式の場合、二重接線を \(y=mx+n\), 異なる2点の\(x\)座標を\(α,β\), とすると
\(f(x)-(mx+n)=(x-α)^2(x-β)^2h(x)\) (\(h(x)\)は整式で、定数のときは\(0\)でない)
と表すことができ、右辺は\(4\)次以上の整式となります。
したがって、二重接線が存在するのは4次以上の関数の場合であり、2次,3次関数では存在しないことになります。
2次、3次関数では二重接線が存在しないために、接点が異なれば接線も異なることがいえます。
(例題)
\(f(x)=x^4-4x^3-8x^2\) とする。曲線 \(y=f(x)\) に2点 \((a,f(a))\) と \((b,f(b))\) (\(a<b\)) で接する直線の方程式を求めよ。
(解答)
\(x\)軸に垂直な直線は接線にならないので、求める接線を
\(y=mx+n\) とおくと
\((x^4-4x^3-8x^2)-(mx+n)=(x-a)^2(x-b)^2\)・・・①
が成り立つ。
(①の右辺)
\(=\{x^2-(a+b)x+ab\}^2\)
\(=x^4-2(a+b)x^3+\{(a+b)^2+2ab\}x^2-2ab(a+b)x+a^2b^2\)
①の両辺の係数を比較すると
\(4=2(a+b)\)・・・②
\(-8=(a+b)^2+2ab\)・・・③
\(m=2ab(a+b)\)・・・④
\(-n=a^2b^2\)・・・⑤
②より
\(a+b=2\)・・・⑥
③に代入して
\(-8=4+2ab\)
\(ab=-6\)・・・⑦
⑥⑦より、\(a,b\)は
\(X^2-2X-6=0\) の2解。
\(a<b\) より
\(a=1-\sqrt{7}\), \(b=1+\sqrt{7}\) (異なる2接点が存在する)・・・(注)
④⑤と⑥⑦より
\(m=-24\), \(n=-36\)
したがって接線の方程式は
\(y=-24x-36\)
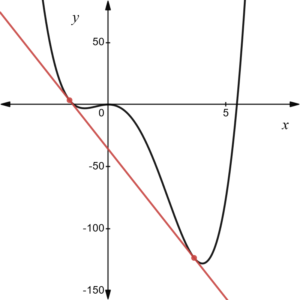
※次数の大きい方から平方完成をする要領で最終的に(2次式)\(^2\)の形を目指すと
\(f(x)\)
\(=\color{blue}{x^4-4x^3}-8x^2\)
\(=(x^2-2x)^2-4x^2-8x^2\)
\(=(x^2-2x)^2-12x^2\)
\(=(x^2-2x)^2-12(x^2-2x)-24x\) (\(x^2-2x\)のカタマリを作る)
\(=\{(x^2-2x)-6\}^2-36-24x\)
したがって
\(f(x)-(-24x-36)=(x^2-2x-6)^2\)
\(x^2-2x-6=0\) は異なる実数解をもつので、その2解を\(a,b\)とすると
\(f(x)-(-24x-36)=\{(x-a)(x-b)\}^2\)
よって接線は \(y=-24x-36\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→法線 back→共通接線②(異なる2点で接する)