接線のなす角に関する問題について見ていきます。
(例題1)
\(a\)を定数とする。2つの放物線
\(C_1: y=-x^2\)
\(C_2: y=3(x-1)^2+a\)
について
(1)\(C_1\), \(C_2\) の両方に接する直線が2本存在するための\(a\)の条件を求めよ。
(2)\(C_1\), \(C_2\) の両方に接する2本の直線が、直交するときの\(a\)の値を求めよ。
(3)\(C_1\), \(C_2\) の両方に接する2本の直線が、\(\displaystyle\frac{π}{4}\) の角度で交わるときの\(a\)の値を求めよ。
(解答)
(1)
2次式なので「接する=重解」の方針で、一方の接点を \((t,f(t))\) とおいて、もう一方の曲線に接する(判別式=0)と考えます。\(C_1\)のほうが式が簡単なのでこちらの接点から始めます。
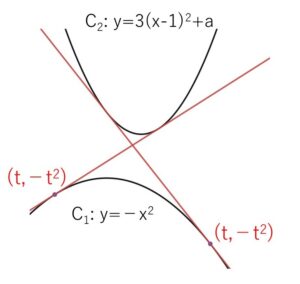
\(C_1: y=-x^2\) 上の点を\(P(t,-t^2)\) とおく。
\(y’=-2x\) より、\(P\)における接線の方程式は
\(y=-2t(x-t)-t^2\)
つまり
\(y=-2tx+t^2\)・・・①
①を \(C_2: y=3(x-1)^2+a\) に代入して
\(-2tx+t^2=3(x-1)^2+a\)
\(x\)について整理すると
\(3x^2+2(t-3)x-t^2+a+3=0\)・・・②
①と\(C_2\)が接するから、②が重解\(x\)をもつので
\((t-3)^2-3(-t^2+a+3)=0\)
\(t\)について整理すると
\(4t^2-6t-3a=0\)・・・③
③が異なる2つの実数解をもてば接線が2本存在することになるので、
\(9+12a>0\)
\(a>-\displaystyle\frac{3}{4}\)
(2)
「傾きの積=-1」を利用します。
\(4t^2-6t-3a=0\)・・・③ の2つの実数解を \(α,β\) とおくと、解と係数の関係から
\(α+β=\displaystyle\frac{3}{2}\)・・・④
\(αβ=-\displaystyle\frac{3a}{4}\)・・・⑤
(④は(3)で使うので出しておきました)
2つの接線の傾きはそれぞれ \(-2α\), \(-2β\) となるので、これが直交するためには
\((-2α)(-2β)=-1\)
⑤より
\(4(-\displaystyle\frac{3a}{4})=-1\)
\(a=\displaystyle\frac{1}{3}\) (\(a>-\displaystyle\frac{3}{4}\)を満たす)
(3)
平行移動してもなす角は変わらないので、2つの接線の交点を原点にくるように平行移動すると、2つの接線の方程式は
\(y=-2αx\), \(y=-2βx\)
\(\tanθ_1=-2α\), \(\tanθ_2=-2β\) とおくと、なす角が\(\displaystyle\frac{π}{4}\) より
\(|\tan(θ_1-θ_2)|=\tan\displaystyle\frac{π}{4}\)
公式そのものを適用するならこのように絶対値をとるということですが、具体的に\(θ_1,θ_2\)の配置を考えると次の通りです。
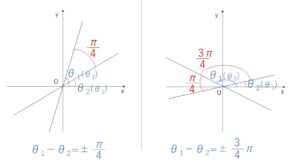
ただし、接点を\(P_1,P_2\)、2接線の交点を\(A\)として、\(\angle P_1AP_2=\displaystyle\frac{π}{4}\) のような問題では、上図の一部が除かれるので、少しだけ違う問題になります。
\(|\tan(θ_1-θ_2)|=1\)
加法定理より
\(\tan(θ_1-θ_2)\)
\(=\displaystyle\frac{\tanθ_1-\tanθ_2}{1+\tanθ_1\tanθ_2}\)
\(=\displaystyle\frac{-2α+2β}{1+4αβ}\)
\(=\displaystyle\frac{2(β-α)}{1-3a}\) (⑤より)
したがって
\(|\displaystyle\frac{2(β-α)}{1-3a}|=1\)・・・⑥
中身の正負で場合分けして絶対値を外しても構いませんが、その際は対称な2解を \(α<β\) としてしまいしょう。すると\(a\)の場合分けだけですみます。
⑥の両辺を二乗して
\(\displaystyle\frac{4(β-α)^2}{(1-3a)^2}=1\)
\(\displaystyle\frac{α^2+β^2-2αβ}{(1-3a)^2}=\displaystyle\frac{1}{4}\)
\(\displaystyle\frac{(α+β)^2-4αβ}{(1-3a)^2}=\displaystyle\frac{1}{4}\)
④⑤より
\(\displaystyle\frac{\displaystyle\frac{9}{4}+3a}{(1-3a)^2}=\displaystyle\frac{1}{4}\)
整理すると
\(9a^2-18a-8=0\)
\(a=\displaystyle\frac{3±\sqrt{17}}{3}\)
\(α+β=\displaystyle\frac{3}{2}\)・・・④
\(αβ=-\displaystyle\frac{3a}{4}\)・・・⑤
の2式において、\(a\)が実数であっても\(α,β\)が実数であるとは限らず、この和と積(の結果)について議論してきたので、\(α,β\)が実数である保証がないので確認する必要があります。
ここで、
\(a=\displaystyle\frac{3+\sqrt{17}}{3}\) は正の数だから、\(a>-\displaystyle\frac{3}{4}\) を満たす。
また、
\(a=\displaystyle\frac{3-\sqrt{17}}{3}>\displaystyle\frac{3-5}{3}>-\displaystyle\frac{3}{4}\)
より
\(a=\displaystyle\frac{3-\sqrt{17}}{3}\) も、\(a>-\displaystyle\frac{3}{4}\) を満たす。
以上から
\(a=\displaystyle\frac{3±\sqrt{17}}{3}\)
(例題2)
放物線 \(y=ax^2\) (\(a≠1\)) を\(x\)軸方向に\(p\),ついで\(y\)軸方向に\(q\)だけ平行移動した放物線\(C_{p,q}\)は 放物線 \(y=x^2\) と2点で交わる。1つの交点は\(C_{p,q}\)の頂点であり、他の交点でにおいては両者の接線は直交する。このような\(p,q\)が存在するような\(a\)の値の範囲を求めよ。
(解答)
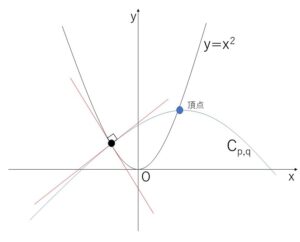
\(C:y=x^2\)・・・①
\(C_{p,q}:y=a(x-p)^2+q\)・・・②
②の頂点は①上にあるので
\(q=p^2\)・・・③
①②より\(y\)を消去すると
\(x^2=a(x-p)^2+p^2\)
(1つの解は\(x=p\)であることを意識して)
\(x^2-p^2-a(x-p)^2=0\)
\((x-p)\{(1-a)x+p+ap\}=0\)
よって\(C_{p,q}\)の頂点以外の交点\(H\)は、\(a≠1\)より
\(x=\displaystyle\frac{p(a+1)}{a-1}\)
2点で2曲線が交わっているので
\(p≠\displaystyle\frac{p(a+1)}{a-1}\)
\(p(a-1)≠p(a+1)\)・・・④
\(p=0\) だと④の両辺が等しくなるので
\(p≠0\)
\(C\),\(C_{p,q}\) の方程式を微分するとそれぞれ
\(y’=2x\)
\(y’=2a(x-p)\)
交点\(H\)における接線が直交しているので
\((2\cdot\displaystyle\frac{p(a+1)}{a-1})\{2a(\displaystyle\frac{p(a+1)}{a-1}-p)\}=-1\)
整理して
\(\displaystyle\frac{8p^2a(a+1)}{(a-1)^2}=-1\)・・・⑤
⑤において、\(a=0,-1\) とすると等式を満たさないので、\(a≠0\), \(a≠-1\)
\(p^2=-\displaystyle\frac{(a-1)^2}{8a(a+1)}\)・・・⑥
\(p≠0\) より \(p^2>0\) であれば⑥を満たす実数\(p\)が存在するので
\(a(a+1)<0\)
\(-1<a<0\)
このとき、\(q=p^2\) より、実数\(q\)も存在する。
答 \(-1<a<0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→関数の増減・極値・グラフ① back→法線