係数決定(極値)

極値に関する関数の係数決定の問題について見ていきます。

(例題1)
関数 \(f(x)=x^3+ax^2+bx+c\) は \(f(-3)=0\) となる。また、\(x=-1\) のとき、極大か極小となり、そのときの極値は\(32\)である。このとき、\(a,b,c\)の値を求めよ。

(解答)
\(f(x)=x^3+ax^2+bx+c\)　において

\(f(-3)=0\) より
\(-27+9a-3b+c=0\)・・・①

また、\(x=-1\) で 極値\(32\)となるから
\(f(-1)=32\)
\(-1+a-b+c=32\)・・・②

\(f'(x)=3x^2+2ax+b\) より
\(3x^2+2ax+b=0\) の解が \(x=-1\) だから
\(3-2a+b=0\)・・・③

①～③より
\(a=-3\),　\(b=-9\)　\(c=27\)

(以下極値をとるか確認作業)

逆に
\(f(x)=x^3-3x^2-9x+27\) のとき

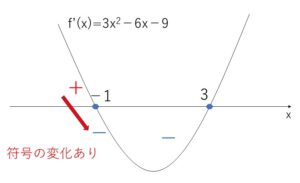
\(f'(x)=3x^2-6x-9\)
\(=3(x+1)(x-3)\)

だから増減表より条件を満たす。

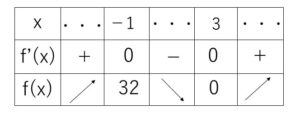
答 \(a=-3\),　\(b=-9\)　\(c=27\)

導関数　\(f'(x)=3x^2-6x-9\) において
\(f'(x)=0\) が異なる2つの実数解をもち、解 \(x=-1\) の前後で符号が変わるという考えでもOKです。

(例題2)
\(f(x)=x^3+ax^2+(a-1)x\) とする。
\(f(x)\) の極大値が\(0\)のとき、\(a\)の値を求めよ。

(解答)
\(f(x)=x^3+ax^2+(a-1)x\) において

\(f'(x)=3x^2+2ax+(a-1)\)

極大値\(0\)をとるときの値を \(x=k\) とすると

\(f(k)=k^3+ak^2+(a-1)k=0\)・・・①
\(f'(k)=3k^2+2ak+(a-1)=0\)・・・②

①より
\(k(k^2+ak+a-1)=0\) だから

\(k=0\) または \(k^2+ak+a-1=0\)

(1)\(k=0\) のとき

②より
\(a-1=0\) だから \(a=1\)
このとき
\(f'(x)=3x^2+2x=x(3x+2)\)
よって
\(x=k=0\) 前後で、\(f'(x)\)の符号が負から正に変わり、極小値となるので不適。

(増減表を書いてもよいです)

(2)\(k^2+ak+a-1=0\)・・・③ のとき

②－３×③より (\(k^2\)を消去する方針)
\(-ak-2(a-1)=0\)
\((k+2)a=2\)・・・④
\(k=-2\) とすると、④を満たさないので、\(k≠-2\)
よって
\(a=\displaystyle\frac{2}{k+2}\)・・・⑤

⑤を③に代入して
\(k^2+\displaystyle\frac{2k}{k+2}+\displaystyle\frac{2}{k+2}-1=0\)
整理して
\(\displaystyle\frac{k(k+1)^2}{k+2}=0\)

(1)より \(k≠0\) だから
\(k=-1\)
⑤より
\(a=2\)

このとき、
\(f'(x)=3x^2+4x+1=(3x+1)(x+1)\)
となるので、\(x=k=-1\) 前後で、\(f'(x)\) の符号が正から負に変わるので、\(x=k\)で極大値となる。

以上から
\(a=2\)

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→絶対値を含む関数の微分　back→関数の増減・極値・グラフ②