微分可能と連続性の関係について見ていきます。
・微分可能と連続
2次関数や3次関数などは、実数全体で連続であり微分可能な関数です。微分可能性と連続性については何らかの関係がありそうですが、微分可能と連続性について次のことが成り立ちます。
関数 \(f(x)\) が \(x=a\) で微分可能ならば、\(x=a\) で連続である。
(解説)
この定理の証明は次のように簡単にできます。
(目標は \(\displaystyle\lim_{x \to a}f(x)=f(a)\))
\(\displaystyle\lim_{x \to a}\{f(x)-f(a)\}\)
\(=\displaystyle\lim_{x \to a}(x-a)\cdot\displaystyle\frac{f(x)-f(a)}{x-a}\)
\(=0\cdot f'(a)\) (微分可能より)
\(=0\)
よって \(\displaystyle\lim_{x \to a}f(x)=f(a)\)
となるから、\(x=a\) で連続である。
ただし、この定理の逆
「関数\(f(x)\)が \(x=a\) で連続ならば、\(x=a\) で微分可能である」
は必ずしも成り立つとは限りません。その典型例は \(f(x)=|x|\) です。
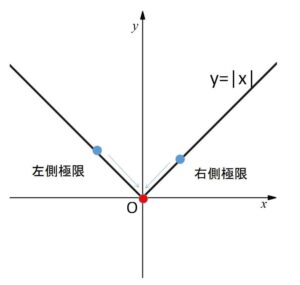
\(f(x)=|x|\) は \(x=0\) で連続ですが、微分可能性については
\(\displaystyle\lim_{h \to +0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{|h|}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{h}{h}\)
\(=1\)
\(\displaystyle\lim_{h \to -0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{|h|}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{-h}{h}\)
\(=-1\)
より、両側で極限が一致しないので \(x=0\) で微分不可です。
なお、この定理の対偶
「関数\(f(x)\)が \(x=a\) で不連続ならば、\(x=a\) で微分可能でない」
は成り立ちます。
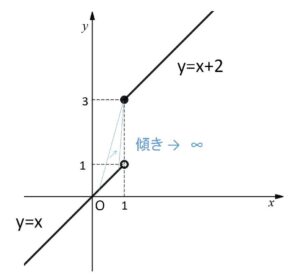
例えば上図の関数については、\(x=1\) で不連続で、一見 \(x=1\) で微分可能なようにも思えますが、微分係数について両側の極限を考えると
\(\displaystyle\lim_{h \to +0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{(1+h+2)-3}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{h}{h}\)
\(=1\)
\(\displaystyle\lim_{h \to -0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{(1+h)-3}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{h-2}{h}\)
\(=+\infty\) (\(\displaystyle\frac{-2}{-0}\) の形)
となり微分不可です。
(例題1)
次の関数\(f(x)\) について
\(\begin{eqnarray} f(x) = \begin{cases} x\sin\displaystyle\frac{1}{x} & ( x≠ 0 ) \\ 0 & ( x = 0 ) \end{cases} \end{eqnarray}\)
(1)\(x=0\) で連続かどうか調べよ。
(2)\(x=0\) で微分可能かどうか調べよ。
(解答)
(1)
\(\sin\displaystyle\frac{1}{x}\) は \(-1\) から \(1\) の間の値しかとらないので、
\(\displaystyle\lim_{x \to 0}x\sin\displaystyle\frac{1}{x}=0\) です。
\(-1≦\sin\displaystyle\frac{1}{x}≦1\) だから
\(-x≦x\sin\displaystyle\frac{1}{x}≦x\)
よって \(x \to 0\) のとき両辺は\(0\)に収束するので、はさみうちの原理より
\(\displaystyle\lim_{x \to 0}x\sin\displaystyle\frac{1}{x}=0\)
ゆえに
\(\displaystyle\lim_{x \to 0}f(x)=f(0)\)
となるから、\(x=0\) で連続である。
(2)
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{h\sin\displaystyle\frac{1}{h}}{h}\)
\(=\displaystyle\lim_{h \to 0}\sin\displaystyle\frac{1}{h}\)
(\(h \to 0\) のとき、\(-1\) と \(1\) を行ったり来たりする)
この極限は存在しないため、\(x=0\) で微分可能でない。
(例題2)
関数\(f(x)\)を次のように定める。
\(\begin{eqnarray} f(x) = \begin{cases} ax^2+bx-2 & ( x≧ 1 ) \\ x^3+(1-a)x^2 & ( x < 1 ) \end{cases} \end{eqnarray}\)
\(f(x)\)が \(x=1\) で微分可能となるように、\(a,b\)の値を定めよ。
1つ目は、「微分可能ならば連続」という定理から、\(x=1\) での連続性より等式が手に入ります。もう1つはもちろん微分係数の存在です(両側極限の一致)。
なお、微分係数の存在については微分の定義を利用しない方法もあります(別解)。
(解答)
\(\begin{eqnarray} f(x) = \begin{cases} ax^2+bx-2 & ( x≧ 1 ) \\ x^3+(1-a)x^2 & ( x < 1 ) \end{cases} \end{eqnarray}\)
\(x=1\) で微分可能なので、\(x=1\) で連続。
よって
\(\displaystyle\lim_{x \to 1-0}f(x)=\displaystyle\lim_{x \to 1+0}f(x)=f(1)\)
より
\(1+(1-a)=a+b-2\ (=f(1))\)
整理して
\(2a+b=4\)・・・①
また、微分係数について
\(\displaystyle\lim_{h \to -0}\displaystyle\frac{f(1+h)-f(1)}{h}=\displaystyle\lim_{h \to +0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
左辺は
\(\displaystyle\lim_{h \to -0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{(1+h)^3+(1-a)(1+h)^2-(a+b-2)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{h^3+(4-a)h^2+(5-2a)h+(4-2a-b)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{h^3+(4-a)h^2+(5-2a)h}{h}\) (①より)
\(=\displaystyle\lim_{h \to -0}\{h^2+(4-a)h+(5-2a)\}\)
\(=5-2a\)
右辺は
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{a(1+h)^2+b(1+h)-2-(a+b-2)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{ah^2+(2a+b)h}{h}\)
\(=\displaystyle\lim_{h \to +0}(ah+2a+b)\)
\(=2a+b\)
ゆえに
\(5-2a=2a+b\)
整理して
\(4a+b=5\)・・・②
①②より
\(a=\displaystyle\frac{1}{2}\)、\(b=3\)
(別解)
\(\begin{eqnarray} f(x) = \begin{cases} ax^2+bx-2 & ( x≧ 1 ) \\ x^3+(1-a)x^2 & ( x < 1 ) \end{cases} \end{eqnarray}\)
\(x=1\) で微分可能なので、\(x=1\) で連続。
よって
\(\displaystyle\lim_{x \to 1-0}f(x)=\displaystyle\lim_{x \to 1+0}f(x)=f(1)\)
より
\(1+(1-a)=a+b-2\ (=f(1))\)
整理して
\(2a+b=4\)・・・①
(ここまでは同じ)
また実数全体を定義域として
\(f_1(x)=ax^2+bx-2\)
\(f_2(x)=x^3+(1-a)x^2\) とおくと、実数全体で微分可能で
\(f_1′(x)=2ax+b\)・・・(i)
\(f_2′(x)=3x^2+2(1-a)x\)・・・(ii)
\(f(x)\)が\(x=1\)で微分可能だから
\(\displaystyle\lim_{h \to +0}\displaystyle\frac{f(1+h)-f(1)}{h}=\displaystyle\lim_{h \to -0}\displaystyle\frac{f(1+h)-f(1)}{h}\)
((i)(ii)は微分可能であることを表しているので両側極限が存在し一致。よって右側(左側)極限は(i)(ii)に\(x=1\)を代入すればよい)
\(f_1′(1)=f_2′(1)\)
\(2a+b=3+2(1-a)\)
\(4a+b=5\)・・・②
①②より
\(a=\displaystyle\frac{1}{2}\)、\(b=3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→導関数の定義と性質 back→微分係数